|
|
 |
t would be natural to suppose that mathematical foundations might begin
with arithmetic, or plane geometry, rather than numbers; after all, everyone
knows what a number is, right? Not so fast: it can be remarkably difficult
to say exactly
what a number is. Go ahead, try it. If you are tempted to say, “it's what
tells you how much or how many of something,” then that's a good effort.
Only trouble is, that's not a definition, but a characterization.
It's like saying, “a chair is something you sit on.” Useful information,
no doubt, but we'd be a bit disappointed if we looked up “chair” in a dictionary
and found no more than “something you sit on.” After all, one can sit on
lots of things that aren't chairs.
The problem of “what is a number,” is an old one. To tackle it, mathematicians in the late 19th and early 20th centuries

Number proceeds
from unity. | | | – Aristotle

|
(particularly Cantor, Dedekind, Frege, Peano, Russell, and Whitehead)
turned to a new (at the time) branch of mathematics called set theory.
They didn't solve the problem, but they developed a beautiful theory which
can be used to model and extend our primitive (i.e., “given” or “intuitively
obvious”) sense of number. A good deal of modern mathematics is now founded
on this work – using, at root, nothing more sophisticated than the set operations
of union and intersection with which you may already be familiar. We'll
be wanting to use these operations shortly, so let's review them now. We
begin with defining the notion of a set:
A set is any well-defined collection of objects.
In other words, any collection considered as a single thing. By “well-defined,”
we mean that we can always tell when something is an element of the set in
question, or when it isn't – no ambiguity. By “object” we mean absolutely
anything: physical objects, ideas, colors, abstractions, and anything else
you care to think of (that can form part of a well-defined collection).
We want to be able to write our sets down, and there
is an established way of doing this. We first designate a symbol to stand
for the set itself, usually a capital letter like A or S or some such. Then, we use (curly) braces to enclose some representation of the elements of the set, as follows:

How do we represent the elements inside the braces? There are two ways.
The first and best is simply to list them. For example, if A is a set of colors, we could write it down this way:
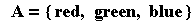
Sometimes, however, listing the elements is not convenient or even possible.
In that case we would use a rule method, using a statement like “all shades
of green,” or even, “all colors” to represent our set.
When something is an element of a set, we denote this with a special symbol (that looks kind of like a curvaceous “E”):
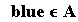
This means, “‘blue’ is an element of the set A.”
Much of the power of set theory arises from the fact that we can form sets whose elements are other sets. For example, if A, B, and C are sets of colors, we could form a set of sets of colors.

Notice that the sets A, B, and C have some elements in common. For instance, A and B both contain the element “blue.” If it happens that every element of a set is also contained in some other set, then we say that the first set is a subset of the other set, and we denote this with a big “U-shape” lying on its side. For instance, if D is the set containing only “blue,” then we could write,
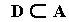
or, equivalently,
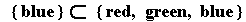
We consider every set to be a subset of itself. (Funny thing to do,
really, but it makes sense, sort of. At least, it matches the definition
of subset.) Also, there is one set that is a subset of every
set, namely the empty set – the set with no elements. This is often denoted
by a circle with a line through it, or a pair of braces with nothing between
them.
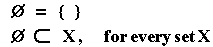
Finally, we are ready for the “set operations” of union and intersection. The union of two sets A and B is the set containing all the elements that are in either A or B. Thus, if A and B are the two sets of colors above, then we have,
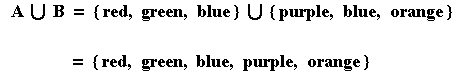
The intersection of two sets is the set containing only elements that are in both. For example, the intersection of A and C would be denoted as follows:
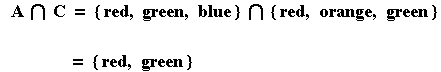
Armed with these ideas, we may now turn to our real purpose – nailing down numbers.
e will begin where every child begins – with counting. The first mathematical
thing we learn to do as children is to say “this many” and hold up our fingers.
When we do this, we mean that there is the same “many” as the “many” of
fingers we are holding up. Then we learn that the “many's” have names, and
are ordered, and slowly we memorize the names and the order they come in
(in base ten), starting with “one, two, three, ... .” These numbers are
called the natural numbers, and are denoted as follows:
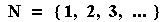
The set of natural numbers is always symbolized by a boldface (or “chalkboard”) capital N, as above. Notice the set notation. This is critical, and provides us with an important characterization:
A number is an element of a set.
Thus, the counting numbers – one, two, seventy-three, a million, and so on – are elements of the set of natural numbers.
The set of natural numbers has some properties that should be noted. First, of course, is that this set is ordered.
This means that, given two different natural numbers, one always comes “after”
the other, and the other comes “before.” (This isn't true, for example,
of the set of colors. One color doesn't “come after” another in any necessary
sense.) This may seem so obvious as to be beneath our notice, but we will
find as we start to really learn mathematics (as opposed to just memorizing procedures) that such niceties can sometimes take on surprising significance.
In fact we can do better with the natural numbers than saying merely
that they are ordered. They have a property that we call being well-ordered:
A set is said to be well-ordered if
every subset of it has a smallest element.
So in other words, given any collection of natural numbers, say for instance { 67, 4, 9, 345, 22 }, then there is always a smallest one in the set (4 in this instance). Notice that there is not always a largest
element; the set of all even numbers, the set of all multiples of 5, and
the set of all the natural numbers greater than 37 are examples of sets that
have no greatest element.
This business of not having a largest element is something
every child notices at some point (and then experiences her or his first
brush with the idea of infinity). We know that there isn't a largest natural
number because, intuitively at least, we know the following principle (which
is sometimes called the Archimedian principle):
If n is a natural number, then n + 1 is a natural number.
Another way of saying this is that the natural numbers are closed under addition. That is, take any two natural numbers and add them, and you get another natural number.
|
GETTING FORMAL
|
|
We can establish in a concrete way that the natural numbers have
no largest element by reasoning as follows: suppose that there was a largest natural number, and let's designate it by B. Then by the principle that you can always add one, B + 1 is also a natural number. Observe that B + 1 is larger than B. But we said that B
was the largest. This is a contradiction, and whenever a chain of reasoning
leads to a contradiction we conclude that one or more of our premises was
false. The only premise in this case was that there does exist a largest natural number, so this must be false, i.e., there does not exist a largest natural number.
|
|
Addition can't take you outside of the set. Notice that the natural
numbers are also closed under multiplication (which makes sense, since multiplication
is just repeated addition).
The natural numbers are the only numbers we need for
one of the most imporant results in classical mathematics, which comes down
to us from antiquity (it is found in Euclid's Elements). This result is called the Fundamental Theorem of Arithmetic, which every numerate person should know.
Students often ask why zero isn't included in the set of natural numbers. Many texts describe a set called the whole numbers,
which is just like the set of natural numbers except that it also includes
zero. This set, however, is not used much, and it is as well to separate
zero conceptually from the natural numbers because it is really a very different
kind of thing. When you count a collection of objects, you don't begin by
saying, “zero, one, two, ... ”, after all. Its historical development is
quite different, too. People were counting for millenia before zero was
ever thought of. (In fact its first use is thought to have been in India
in the 6th or 7th century, and came to us – like so much of the mathematics
that we use in the western world – by way of Arabic culture in about the
11th century. It's notable that native Americans, specifically the Mayan
civilization, also developed a concept of zero independently of the old world.)
So anyway, we don't include zero in the natural numbers. We will find it,
however, in our next set...
 |
e said that the set of natural numbers is closed under addition and multiplication,
but of course there are other operations with numbers. Subtraction, for
instance. If we take away two from three, then there is no problem because
the remainder is one, and one is in the set of natural numbers. What happens,
however, if we want to go the other way and take three from two? We get
a negative number, and negative numbers aren't included in the set of natural
numbers. In order to talk about negative numbers, we will need to introduce
a new set:
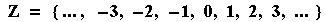
This is the set of integers, and is always denoted by a bold faced Z. (The Z is from the German word zahlen,
which means “to count.”) Notice that it includes all the natural numbers,
zero, and all the negatives of the natural numbers. This means the natural
numbers are a subset of the integers, i.e.,
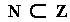
Historically, negative numbers didn't come into wide use until the late middle ages, circa
the 14th century. Before that time, negative quantities weren't considered
“real,” and so it was thought that one shouldn't try to calculate with them.
After all, when did you last see a negative quantity? No one is “minus
five feet tall,” for instance. However, negative numbers can be very handy
for calculations involving debt, and the Italians (who invented banks) were
the first to recognize their importance in finance and to use them for that
purpose.
he integers are closed under addition, subtraction, and multiplication,
but what about division? If we divide two into four we're all right, but
what about dividing two into three? Then we get catapulted right out of
the integers and into the world of ratios, or rational numbers.
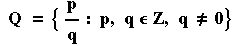
This looks much more complicated than anything we've done before, but
don't be alarmed – we'll take it apart piece by piece. What it says is,
the set of rational numbers is the set consisting of all numbers of the form
p divided by q, where p and q are elements of the set of integers and q is not zero.
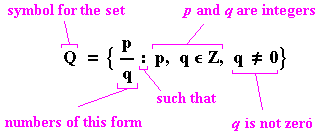
This is an example of using the “rule method” to designate the elements
of a set, rather than the “list method” we used before.
|
WHY NOT?
|
|
What makes giving a "list" of the rational numbers difficult is their denseness: Suppose a and b are rational numbers. Then, since the rational numbers are closed under addition and division, the number (a + b)/2 (the average of a and b) is also rational, and it lies between a and b. Thus, between any two rational numbers you can find another one. This is what "dense" means in this context. Although, as we show in the Infinity MiniText,
it really is possible to make a one-after-the-other list of the rational
numbers, no such list is really suggestive of the entire set in an unambiguous
way.
|
|
We need to use the rule method because there is no way to “list” rational
numbers that suggests the complete list in an unambiguous way. Even using
an elipsis ( ... ) doesn't help.
Historically, the rational numbers are nearly as old
as the natural numbers. They go all the way back to the ancient Babylonians
and Egyptians, and the Greeks were particularly fond of them (though none
of these cultures used our notation, which is Arabic). The Pythagoreans
of ancient Greece even believed that everything in creation could be understood
and analyzed in terms of natural numbers and their ratios. (As we'll see
below, this idea wasn't to last – it's days, so to speak, were numbered!)
Notice that the natural numbers and the integers are
both subsets of the rational numbers, since any integer can be expressed
as a ratio:
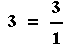
The rational numbers are closed under all the arithmetic operations,
and if all we ever needed to do was arithmetic we'd never need any other
numbers at all. However, sometimes we need more than arithmetic to construct
adequate models of the world around us. For this reason, much of the work
we do in mathematics will require us to add to the rational numbers a new
set – a set of numbers which is the topic of our next section.
n addition to their fascination with numbers and ratios, the Greeks were
very keen on geometry. Among the most important results in all of mathematics
is the famous Pythagorean Theorem:
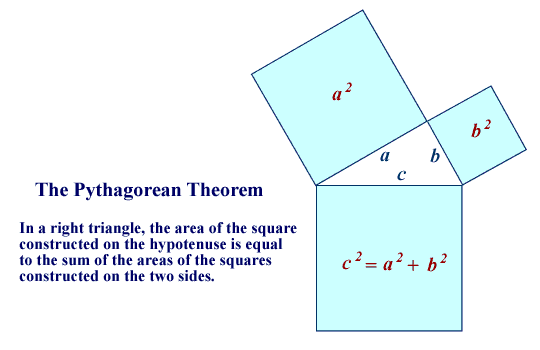
This theorem and its many important uses wants a mini-text all its own,
but for now let's just apply it to a simple square with sides of length one,
and ask the obvious question, “how long is the diagonal?”
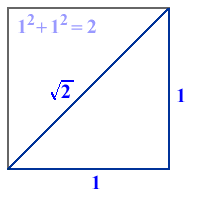
We see that the length of the diagonal is the square root of two, since
one squared plus one squared is two, so the length of the diagonal squared
is equal to two.
SO . . . is the square root of two a rational number?
That is, can it be written as the ratio of two integers? Remember that
the Pythagoreans believed that everything was either a whole number or a ratio. In fact, it turns out that the square root of two cannot be written as a ratio of integers – it is irrational. (How do we know?)
Note that “irrational” doesn't mean crazy or unreasonable; it means “not
expressible as a ratio (of integers).” Legend has it that when the Pythagoreans
(who were at sea at the time) first heard about it, they were so overcome
by their feelings that they took the poor man who discovered this fact and
threw him overboard, drowning him.
The upshot is that we need more than just rational
numbers if we wish to work with many kinds of abstract quantities, such as
length and proportion in idealized space, for instance. We need irrational numbers too. We don't tend to bother much about the set of irrational numbers (usually denoted by a bold-faced I
) in and of itself, but focus instead on what we get when we mix the rationals
and the irrationals together: that most beautiful, strange, and wondrous
of sets, the real numbers.
 |
e said above that the set of real numbers is obtained by collecting together
the rational numbers and the irrational numbers, i.e.,
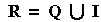
Thus, every rational number is a real number, and every irrational number
is a real number. The real numbers, taken all together, form what is called
a continuum.
They are closed under all the arithmetic operations, and they are also closed
“geometrically.” This last point is important, because it means that we
can use geometrical pictures to represent the real numbers and vice versa. The principal and most useful picture we use is called the real number line, and will no doubt be familiar:
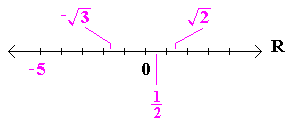
Here, every point on the real number line corresponds to a unique real
number, and every real number corresponds to a unique point on the line.
We see that the real numbers are totally ordered, and include every kind
of number we might need. A beautiful set.
Notationally, we often represent real numbers using
decimal notation, in which we write a real number as its integer and non-integer
parts, separated by a dot. Notice that the non-integer part is actually
a sum of fractions: so many tenths, plus so many hundredths, plus so many
thousandths, and so on.

If the decimal terminates, then it represents a rational number. This
is also true if the decimal repeats the same pattern endlessly. In this
latter case, we represent the “endlessly repeating pattern” by putting a
line over the repeating part.
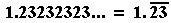
However, if the decimal continues forever without falling into a pattern
that repeats endlessly, then it represents an irrational number. Obviously,
one cannot write down an endless sequence of digits, so we just use an ellipsis
after a few digits to represent that the sequence continues.
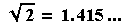
Notice how unimaginably dense
the set of real numbers is! We already knew that the rational numbers were
dense, in that between any two you could find another, but now consider the
irrationals – are they dense, or what? Just as we can find a rational
number between any two rational numbers, so we can find as many irrational
numbers as we please between any two rational numbers (or irrational numbers).
To see this, take two rational numbers (in decimal representation) that
are very close together. Then we can do the following:

Infinities within infinities . . . .
The real numbers have many properties that are both useful and surprising,
as you will discover in your continued study. Indeed, an immense body of
mathematical science is devoted to these properties, particularly the field
of real analysis.
There are other numbers sets, as well; the imaginary numbers, the complex
numbers, the infinitessimals, and so on. There are even numbers called “hyperreal”
and “surreal.”
Indeed, this article merely scratches the surface of
“number.” Even the natural numbers themselves, the ones we learn to count
with as toddlers, harbor within their depths great riches. It is not for
nothing that the great mathematician Karl Gauss called number theory (the science of the natural numbers) the “Queen of Mathematics.” A good place to start is with the suggested readings below.
Numbers are the highest degree of
knowledge. It is knowledge itself.
– Plato
|



![]()
![]()
![]()

![]()
![]()
![]()
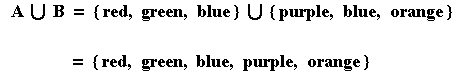
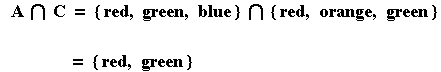
![]()
![]()
![]()
![]()
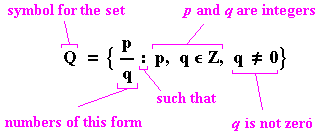
![]()


![]()


![]()
![]()


