None to speak of, although you should recall the definitions of the trig
functions (in terms of ![]() and
and ![]() ).
).
Trigonometric identities are essentially theorems with well-known proofs. Among the most important are the following:
-
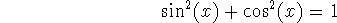
(Pythagorean theorem). If we divide this by either
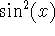 or
or 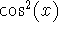 ,
we get a new identity involving
,
we get a new identity involving 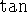 and
and 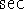 , or
, or 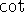 and
and 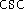 .
. -
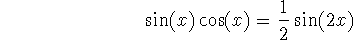
(double angle formula), from which we can derive a formula for
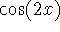 by
using the Pythagorean identity.
by
using the Pythagorean identity. -
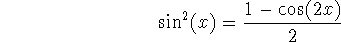
(half-angle formula), from which we can derive a formula for
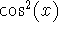 by
using the Pythagorean identity:
by
using the Pythagorean identity:
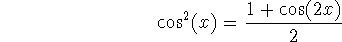
-
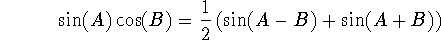
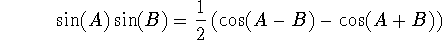
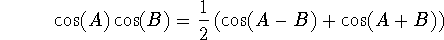
You might wonder what's so exciting about these types of integrals: it turns out that they occur in an essential way in an important technique called Fourier analysis. The idea is that we can approximate relatively arbitrary functions in terms of trig functions, but we won't go into that now (hints of it in problem #66, p. 517, however!).
This section might be considered ``archaic'' by some: it's full of techniques which we really don't need much anymore, since, if we're confronted by some hairy integral of this class we would be able to get the solution most easily by asking your TI calculator to solve it...!
One of the important lessons of this section is the usefulness of trigonometric identities, many of which you've undoubtably forgotten. Take this opportunity to remember the relationship between tan, sec, sin, and cos, etc., and their derivatives.