-
integration by parts:
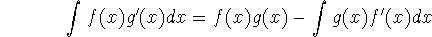
or
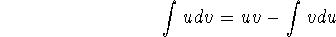
None to speak of. In fact, this is essentially a corollary of the Fundamental Theorem of Calculus.
The biggest hint is simply that this integration technique, like all integration techniques, is really just a differentiation technique in reverse.
Integration by parts may need to be carried out multiple times: sometimes the idea is to simplify the integral each time, until a really simple one arises allowing us to calculate the final solution (e.g. Example 6, p. 507). Sometimes it's something of a trick: we compute the integral multiple times in order to return to the original integral, allowing us to solve an equation for the original integral (e.g. Example 4, p. 506).
We encounter integration by parts, which is a way of turning one integral into another that we prefer to integrate by using the product rule in reverse. Similarly, and as mentioned in the text, substitution is really just the chain rule in reverse. Integration and differentiation are inverse processes. One of the differences, however, is that whereas the derivative of a function is unique, the indefinite integral of a function represents a class of functions.