
#2. This student paid me a visit, and I suggested that, while I didn't need these proven in all generality, I would like to see them proven for at least one case of, say, a < b < c (we actually need to consider permutations of these, too).


This student got a "tilda" because this should be more general than
indicated. The number "0" is not our only choice for the "0" of the
(prospective) Boolean algebra. Hence we might say "Let m be the zero;
consider x=m-1:
By the way: one may not invoke duality for these problems, unless duality applies to the min/max: we don't have a Boolean algebra, as part b shows! Hence, duality is not to be assumed.
#10.
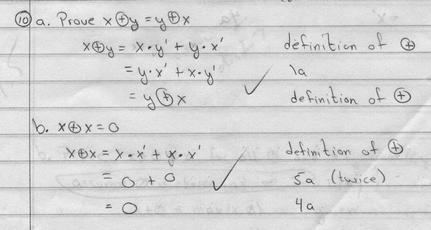
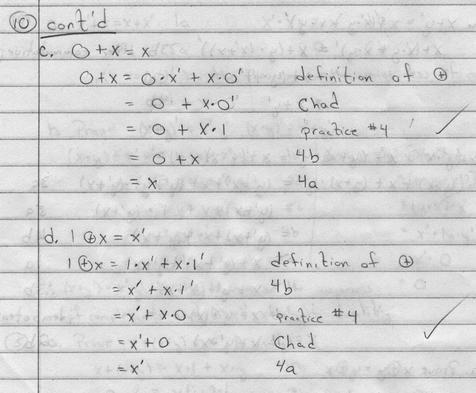
The subtlety that this student picked up on that many others forgot is that one
must justify the step
Part c. shows a problem several students had: you need to explicitly indicate that we're talking about "circle-+" in the first and second lines - a binary operation different from the "+" of the Boolean algebra.