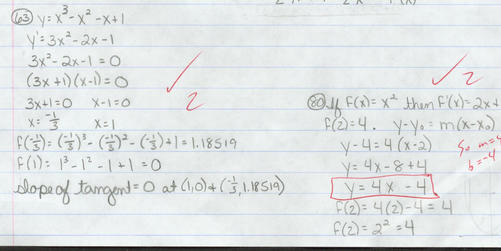
problem #63: Seeking points at which the tangent lines to the curve have zero slope is equivalent to seeking roots (or zeros) of the derivative function. Remember that you are asked to give the points on the curve at which the tangent is horizontal - hence you should give ordered pairs, e.g. (1,f(1))=(1,0).
problem #80: This is a novel approach (see my "traditional" approach below): the student says that the quadratic has a known location and slope at x=2, so that the linear function mx+b will have to match it. But given a point and a slope, the linear function is fully determined! Good thinking....
