- function - a rule which assigns to each input of the function's domain a unique output in the function's range.
- domain - the collection of all possible arguments (or inputs) to a function.
- range - a set containing the collection of all values a function produces for all the elements of the domain.
- The value of f at x is the result of feeding x to the function machine f.
- independent variable - a variable which represents the elements of the domain (usually plotted on the horizonal axis).
- dependent variable - a variable which represents the elements of the range (usually plotted on the vertical axis).
- graph - a set of ordered pairs of the form (x,y) or (x,f(x)), which we usually think of as a plot or visual representation of a function.
- piece-wise defined function - whose formula is different for different parts of its domain.
- absolute value function - a function which gives the distance of its argument from the origin; since it's a distance, it's always positive!
- step-function - whose graphs go up or down like stair steps.
- even function - symmetric with respect to the vertical y-axis: f(-x)=f(x).
- odd function - symmetric with respect to the origin: f(-x)=-f(x).
- mathematical model - a mathematical function (or other object) which models some aspect of the real world.
- scatter plot - generally a plot of ordered pairs of points, where we imagine that there is a functional relationship between the two variables. Because of errors in the data, a scatter plot may fail to satisfy the vertical line test.
-
increasing function: when
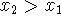 ,
, 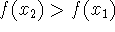 .
. -
decreasing function: when
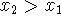 ,
, 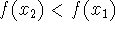 .
.
There are no explicit theorems in this chapter, although the vertical line test is really a sort of theorem: it tells us that a graph without multiple intersections with any vertical line represents a function (and that a graph 01with two intersections with a vertical line is not a function).
There are (at least) four representations of a function:
- verbal
- numeric (e.g. tables)
- visual (e.g. graph)
- algebraic (e.g. formula)
Convention: If a function is given by a formula and the domain is not stated explicitly, the convention is that the domain is the set of all numbers for which the formula makes sense.
This section reviews the definition and properties of functions, and presents four ways to represent them (noted above). Properties studied include symmetry, monotonic behavior (increasing or decreasing), and the piece-wise definition of a functions. Some attention is paid to the vertical line test for whether a graph represents a function y=f(x), and to modeling real-life data with formulas.