Section Summary: 2.2

1. Definitions
   • The concept of a limit - denoted, for example, as

     

     which we read as ``the limit of f as x approaches a is L''. It means that the closer x gets to a, the more f(x) tends to the value L (but we don't let x take on the value a). This may be denoted

     

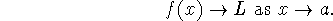
   • One-sided limits: as we see in the examples, a limit may fail to exist as a whole at a, but exist to one side or the other.
     • left-hand limit:

       

       means that as a is approached from the left (i.e. from values less than a) the function values approach L).

     • right-hand limit:

       

       means that as a is approached from the right (i.e. from values greater than a) the function values approach L).

   • Infinite limits: our author says that a limit can fail to exist because the function becomes arbitrarily large (in either a positive or negative sense). In spite of this fact, the notation used seems to imply that the limit does exist:

     • 

       means that as a is approached from either side, the function gets increasingly large and grows in an unbounded manner.

     • 

       means that as a is approached from either side, the function gets arbitrarily large in a negative sense.

     We will say that ``the function goes to infinity'', or that ``the function goes to negative infinity''.

   • Vertical asymptote - if a limit is infinity as 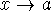, , 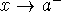or 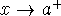, then the graph will tend toward the vertical line x=a (called a vertical asymptote to the graph).

2. Theorems

   

3. Properties/Tricks/Hints/Etc.
   • It doesn't matter what's actually happening to f at a, in

     

     The limit is only concerned with the behavior of f near a: f(a) could exist or not exist as far as the limit is concerned.

   • Example 2 (p. 74) shows that the calculator is not infallible.

   • Tabular data (functions defined as tables, for example) do not lend themselves to limits. The idea of limit simply doesn't apply. On the other hand, we may want to construct a model from the data for which the concept of limit applies, meaning that the data suggested a smooth underlying function.

4. Summary

   We are introduced to the limit in several different flavors: one-sided limits, infinite limits, and the old standby

   

   The idea is to explore the behavior of the function f as its argument x gets arbitrarily close to a fixed number a (but x doesn't actually reach a). f can be smoothly tending towards L, have a jump at L, or could even be infinite as x approaches a (in which case L would be , leading to a vertical asymptote at x=a).