-
tangent line - the line through a point on a graph, P(a,f(a)), with
slope
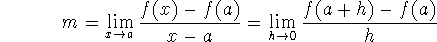
provided the limit exists. [What could possibly go wrong? Well, the function might not be defined at a - i.e., f(a) is undefined; or the function might not be continuous, so that the numerator doesn't tend to 0 (whereas the denominator always does).]
The second definition is obtained from the first via a change of variables: if we replace the independent variable x by the independent variable h, linking them by a shift - x=h+a - then we get the second form of the definition.
-
slope of the curve at a - the slope m of the tangent line at point
P(a,f(a)). Slope is a concept we've associated with straight lines, not with
curves. This gives us a way of associating the idea with curves.
-
position function - s=f(t) - the location of an object as a function
of time. Sometimes we represent it as s(t). Of course, what letter we
associate with it (s versus f versus any other letter) is irrelevant: it's
just a symbol we prefer to use....
-
instantaneous velocity
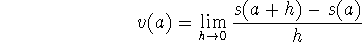
(the slope of the tangent line to the graph of the position function at P(a,s(a))). We can think of this as our first (and one of our most important) examples of the use of this limit.
-
increment of x - the change in x:
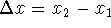 (usually
considered to be a small quantity - that is, the two points
(usually
considered to be a small quantity - that is, the two points 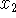 and
and  are
considered to be close together).
are
considered to be close together).
-
average rate of change -
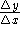 - the slope of the
secant line connecting two points on the graph,
- the slope of the
secant line connecting two points on the graph, 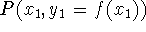 and
and
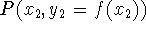 ). This is often used as an approximation to the
instantaneous rate of change.
). This is often used as an approximation to the
instantaneous rate of change.
instantaneous rate of change -
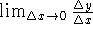 .
.
I didn't find any theorems in this section.
-
There were some nice examples of rates of change from the areas a student is
likely to consider for employment someday:
- From physics: power - rate of change of work with respect to time
- From chemistry: rate of reaction - rate of change of chemical concentration with respect to time
- From business: marginal cost - rate of change of cost of production with respect to some variable x.
- If the tangent line exists, then as we zoom in on the graph at the point P(a,f(a)), we discover that it the graph of the function and the graph of the tangent line seem to become indistinguishable.
Here we catch a glimpse of the importance of limits: they are used to define instantaneous velecity and other important rates of change, which prove important in the sciences, engineering, and the social sciences (e.g. power in physics, rates of reaction in chemistry, and marginal costs in business). Furthermore, we should note that the definition of these slopes involves a limit of a quotient whose denominator has a limit of 0: hence, a trick (e.g. simplifying the numerator, or rationalizing) will be necessary in order to evaluate the limit.
Things observed in the course of working problems.
-
TI hint: Use solve(
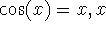 ) to find a solution to this equation.
) to find a solution to this equation. -
Note:

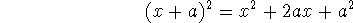
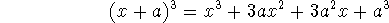
The coefficients of each term come from Pascal's triangle:
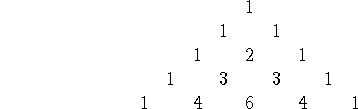
-
TI hint: Use expand(
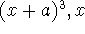 ) to expand out this cubic term.
) to expand out this cubic term. -
TI hint: Use factor(
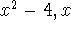 ) to factor an expression.
) to factor an expression.