None!
-
The Chain Rule If f and g are both differentiable, and
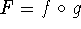is the composite function defined by F(x) = f(g(x)), the F is
differentiable and 
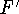is given by the product
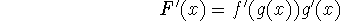
In Leibniz notation, if y=f(u) and u=g(x) are both differentiable functions, then
This is the secret to differentiating composite functions. You definitely need to memorize this formula.
-
The Power Rule combined with the Chain Rule
If n is any real number and g(x) is differentiable, then
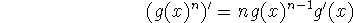
This is simply an example of the chain rule, where the outer function is a power function. It's such an important and common example, however, that you should consider memorizing it separately.
Hmmmm....
The chain rule is the secret to differentiating compositions of functions, and this is a terribly important rule which you must memorize and understand.
The hardest thing about the chain rule is probably identifying the composition
of functions. Given an expression, e.g. 
, you need to realize that
, and g(x)=2x-1 (then apply the rule correctly, of course:
Sometimes we talk about ``outer function'' and ``inner function''. The inner function is the first function x meets on its transformation. The inner function returns a value u, which serves as the input to the outer function which returns a value y. The composite function of inner and outer thus takes a value x and returns a value y.