-
antiderivative - A function F is called an antiderivative of f on
an interval I if
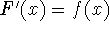for all x in I.
That is, f is the derivative of F, so F is an antiderivative of f: more than one function has f for its derivative. The relationship is not ``monogomous''!
-
differential equation - an equation involving a function f and its
derivatives.
The point of such equations is that we are seeking a function whose derivatives satisfy a particular relationship with it; for example, a function whose second derivative is equal to the negative of the function itself (whose acceleration is equal to its position, but opposite in sign). The sine function satisfies this constraint.
-
direction field - a ``graph'' indicating the trend in a function, based
on its derivative.
If F is an antiderivative of f on an interval I, then the most general antiderivative of f on I is
where C is an arbitrary constant.
As we said, the relationship is not monogomous: f has lots of antiderivatives, whereas each function has its unique derivative.
A short table of antiderivatives is begun on page 300. In the old days, whole huge books of such antiderivatives were published and frequently consulted by mathematicians. Still are, in many cases, although computer software has essentially made them obsolete.
There are certain standard anti-derivatives that one needs to be aware of: for
example, the anti-derivative family of 
is
An antiderivative of f is simply a function which has f for its derivative. We've seen that lots of functions have f for a derivative, but that they vary by very little: a constant, for the most part.
This chapter has us ``thinking backwards'', and this is a skill which takes times and practice to master. Whereas differentiation is essentially a mechanical exercise, antidifferentiation may require insight, and broad exposure to lots of different functions. One asks oneself, ``do I know a function whose derivative looks like this?'' Starting from the derivative(s), and perhaps initial conditions (e.g. the value of the function at a point), we may be able to use direction fields to trace a pretty good representation of the function, and then deduce a formula from that.