-
means that as x gets arbitrarily large, the function value f(x) tends to (in fact, get's arbitrarily close to) the number L. Similarly,
means that as x gets more and more negative, the function value f(x) tends to the number L. The notation
is used to indicate that the function becomes arbitrarily large as x becomes large (and similarly for the limits involving
).
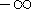We're interested in the behavior of the function at its extremes, far from 0. This is very common in many areas of business or science: in astronomy, for example, when we're looking at the effects of Earth's gravity on a spaceship near the sun (it's essentially negligable - i.e., Earth's gravity(great distance) is about 0:
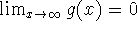). - horizontal asymptote: if either of the two limits above hold, then the line y=L is called a horizontal asymptote of the curve y=f(x).
-
Precise definitions of these limits are also provided:
-
Let f be a function defined on
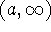. Then
means that for every
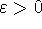there is a corresponding number
N such that
-
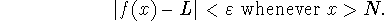
Let f be a function defined on
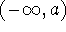. Then
means that for every
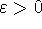there is a corresponding number
N such that
-
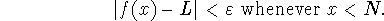
Let f be a function defined on 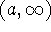. Then
means that for every M > 0 there is a corresponding number N such that
,
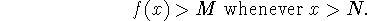
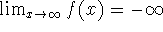etc.
-
Let f be a function defined on
-
If r>0 is a rational number, then
If, furthermore,
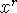is defined for negative numbers, then
-
Most limit laws hold if
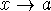is replaced by 
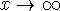or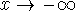 
. - A graph may tend toward a horizontal asymptote in several different ways (e.g. directly from above, directly from below, or by oscillating back and forth).
-
To evaluate limits of rational functions as
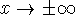, simply divide
numerator and denominator by the highest power of x, and evaluate the limit.
Section 4.4 provides us with intuitive and formal definitions of infinite
limits (that is, as the independent variable x tends toward negative or
positive 
). The notion of a horizontal asymptote is introduced, which
is a horizontal line towards which the function tends. This allows us to
effectively replace a function, which may be rather complicated, by a
number when we get to extreme values of x.
An example of this use of approximation is the force of gravity: it's usually given as 9.81 meters per second squared, and we don't generally ask our distance from the center of the Earth. Gravity falls off as you get farther from the surface of the Earth, toward zero, but this change is so gradual that we treat this force as a constant. If we got far enough away from the Earth, we might treat its force of gravity as another constant - i.e. 0! That is the limit of Earth's gravity as we get ``infinitely far'' away (as if we can!).