none.
First derivative test for absolute extreme values Suppose that c is a critical number of a continuous function f defined on an interval I.
-
If
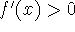 for all x<c and
for all x<c and 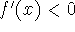 for all x>c, then f(c)
is the absolute maximum of f on I.
for all x>c, then f(c)
is the absolute maximum of f on I. -
If
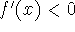 for all x<c and
for all x<c and 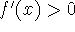 for all x>c, then f(c)
is the absolute minimum of f on I.
for all x>c, then f(c)
is the absolute minimum of f on I.
Steps in solving optimization problems:
- Understand the problem - read carefully: what is the unknown? What are the given quantities? What are the given conditions?
- Draw a diagram. (This is the most important step!)
- Introduce suitable notation. Use symbols that represent the quantities of interest (e.g. h for height, etc.), rather than just x or y.
- Express the dependent variable as an equation in terms of the independent variable(s).
- If there is more than one independent variable, use the relationships among the variables and conditions to solve for the others in terms of a single variable.
-
Find the desired minima or maxima.
This section is the heart of calculus for me. There is something wonderful about being able to determine the best shape of a can to minimize the use of materials, or to discover that if you want Fido to have the biggest pen area given a rectangular fence, then it should be square. This is marvellous stuff!
Take to heart the recommendations for solving these optimization problems (in particular, draw a picture!). Word problems are notoriously difficult, so turn them into picture problems to make them easier to solve!