Newton's method (or the Newton-Raphson method): a method for finding the
roots, or zeros, of a function (i.e., those values of x such that
f(x)=0). The method is based on the linearization of a function: we find the
tangent line to a function at a point ![]() , and find where it
has a root: we hope that this root is closer than
, and find where it
has a root: we hope that this root is closer than ![]() to the true root,
r.
to the true root,
r.
Often these roots are simply approximations of the true roots, but may be good enough for our work. The method is based on the iterative formula
![]()
and a good initial guess (denoted ![]() , pronounced ``x-not''). From
, pronounced ``x-not''). From ![]() we calculate
we calculate ![]() ; from
; from ![]() we compute
we compute ![]() ; etc. If the sequence
converges to some finite number, i.e.
; etc. If the sequence
converges to some finite number, i.e.
![]()
then we have a root r of the function (as a check, compute f(r)).
To find a root to a given degree of accuracy (say five decimal places), we
compute using the iterative formula until the successive iterates ![]() and
and
![]() agree to five decimal places.
agree to five decimal places.
None.
Newton's method may fail for various reasons:
-
The root of the linearization may be farther from the true root than the
original guess
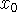 ; it may even fall outside the domain of the function.
; it may even fall outside the domain of the function. -
The derivative
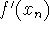 may be equal to 0 for some step n, which makes the
formula undefined.
may be equal to 0 for some step n, which makes the
formula undefined. -
The derivative
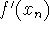 may be equal to
may be equal to 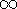 for some step n, which makes
the formula stall at
for some step n, which makes
the formula stall at 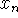 .
. - Newton's method can get into an ``infinite loop'', in which it simply cycles between several values, never approaching the actual root r.
-
The function may not be differentiable at a point
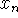 , making the formula
undefined.
, making the formula
undefined. - The succession of iterates tend to infinity (fail to converge).
- The root is at an inflection point where the concavity changes from concave down to concave up.
- And, finally, the best reason for failure: there is no real root!
Suppose that we seek the roots of f(x). The book suggests that the graph of
f(x) and Newton's method may be used in tandom: the graph will provide a good
starting guess ![]() , and Newton's method will provide a good approximation.
, and Newton's method will provide a good approximation.
We are introduced to Newton's method for computing roots of a function, based on the linearization of the function. Once again, we replace a function by a closely related linear function, hoping that the linear function will inform us about the function itself. Linear functions are the simplest interesting functions we have, and they pop up constantly in mathematics (e.g. the slant asymptotes described in section 4.5 are good replacements for the original functions far from the origin).
Newton's method is an iterative method, meaning that we do the same thing over and over, and hope that results get successively better. This is quite likely the basic method on which your calculator's ``solve'' command is based.
It is possible to find different roots from different starting points, in the event that there are multiple roots (e.g. a quadratic equation may have two, etc.). This method often gives a good approximation, but there are a variety of reasons for why Newton's method may fail.