-
area of a region - when computing the area under a curve, we approximate
the area using rectangles, and hope that by using finer and finer rectangles
and letting the area of the rectangles go to zero we arrive at a limit:
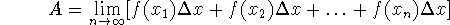
where the
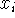are endpoints of the rectangles (e.g. left endpoints, right
endpoints). Note that this means that
(or that the width of the rectangles goes to zero).
-
sample points - In the area definition, we took endpoints and used them
to approximate the integral. But we're not obligated to use those. Since the
rectangles are shrinking, those points are merging. Instead of either right or
left endpoints, we can take any points (sample points) inside the
rectangles, so that the area is approximated by
-
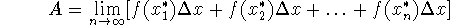
sigma (or summation) notation - we need to write ugly sums like those
above in some nicer way (otherwise mathematicians would have all gotten carpal
tunnel a long time ago!). So we do it this way:
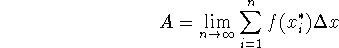
and we might say ``the sum from i=1 to
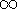of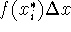 
''.
i is called an index, or a dummy variable. It steps over the integers from 1 to n - while n, in this case, just keeps on steppin'!
- There are two apparently different problems featured in this section: the area problem, and the distance problem. These problems are related, however, with the velocity problem as an example of an area problem. As our text notes, lots of physical problems can be considered as area problems.
- We use approximation methods to compute the areas, using rectangles to approximate the areas under the curves. As these rectangles become finer, the approximation gets closer to the true value. In the limit, we have the area (this is, in fact, the definition of the area).
- Summation (or sigma) notation is introduced, to make the computations easier to represent.