-
Fresnel function:
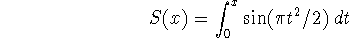
Named after Augustin Fresnel (1788-1827), famous for his work in optics. The Fresnel lens was a miraculous improvement in lighthouse technology: it allowed them to cast a much more powerful beam, and saved many ships and sailors from Davy Jones's locker...
-
Fundamental Theorem of Calculus, Part I
If f is continuous on [a,b], then the function g defined by
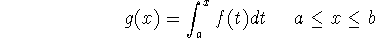
is continuous on [a,b] and differentiable on (a,b), and g'(x)=f(x).
g is undoubtably one of the oddest functions we have seen so far: it is defined as an integral. Symbolically we might write
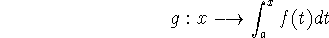
It is a map from the real numbers, represented by variable x, into the real numbers (the values of the integral).
-
Fundamental Theorem of Calculus, Part II
If f is continuous on [a,b], then
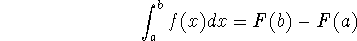
where F is any antiderivative of f: that is, a function such that F'=f.
The big news is that if you know an antiderivative of integrand f, then computing an integral is easy.
-
Fundamental Theorem of Calculus
Suppose f is continuous on [a,b].
-
If
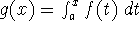 , then g'(x)=f(x).
, then g'(x)=f(x).
-
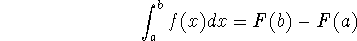
where F is any antiderivative of f.
-
If
-
An important example of this relationship between the function and its
antiderivative is given from the physics of integrating velocity:
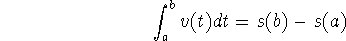
the result is the position function.
-
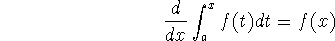
This section introduces the fundamental theorem of calculus. It contains two parts: it shows that integrals are solved using antiderivatives, and that derivatives of functions defined using variables limits are solved using derivatives:
Suppose f is continuous on [a,b].
-
If
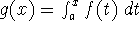 , then g'(x)=f(x).
, then g'(x)=f(x). -
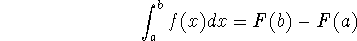
The key is ``variable limits'': for these functions, the variable is in the in the limits of integration (not in the integrand). One problem, or common reason for misunderstanding, is that there is a ``dummy variable of integration'' in the problem. The variable t in the integral
![]()
is a dummy variable: you notice that t doesn't appear on the right hand side: only x appears, because t has disappeared during integration.