-
indefinite integral: represents the antiderivative of a function, so
that
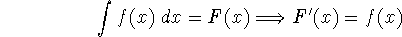
Remember that a definite integral has limits of integration, so that it represents a ``definite area'' (which is a number); the indefinite integral represents a function. One way we represent this is as follows:
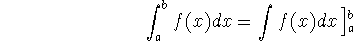
We might read this as ``the integral of f from a to b is equal to an antiderivative evaluated at b minus the same antiderivative evaluated at a.''
Total Change Theorem: The integral of a rate of change is the total change:
We add up all the small changes in the function F from a to b to discover what the total change was in the function F.
-
``We adopt the convention that when a formula for a general indefinite integral
is given, it is valid only on an interval.'' Thus, we write
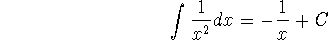
even though the general antiderivative of
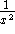is best given by
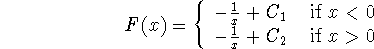
The definition of the indefinite integral emphasizes the close relationship between differentiation and integration. These two processes are inverses of each other, in much the same way that the square root is the inverse process of the square.
The indefinite integral is a function (or, more accurately, a family of functions), whereas a definite integral is a number (representing a fixed area). Furthermore, notice that the ``dummy variable of integration'' (x) is used as the variable of the antiderivative, e.g.
This is a point of confusion for many students. Remember, however, that ``a rose by any other name would smell as sweet'', and that F(t), F(x), F(nose), and F(rose) all represent the same thing: these variables are just place holders.