The substitution rule: If u=g(x) is a differentiable function whose range is an interval I and f is continuous on I, then
Substitution hence refers to a substitution of one variable for another, a change which simplifies the original integral. When all is said and done, however, and we've solved the latter integral to create a function of u, then we need to back-substitute to end with a function of x.
The substitution rule for definite integrals: If 
is
continuous on [a,b] and f is continuous on the range of u=g(x), then
where F is an antiderivative of f.
Suppose f is continuous on [-a,a].
-
If f is even, (that is, f(-x)=f(x)), then
-
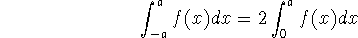
If f is odd, (that is, f(-x)=-f(x)), then
(that makes life easy!).
``Finding the right substitution is a bit of an art. It's not unusual to guess wrong; if your first guess doesn't work, try another substitution.'' (p. 358)
The substitution rule is based on the chain rule from differentiation days. As we've seen in recent days, integration is like differentiation, only backwards: instead of thinking ``Hmmm...here's a function F: what's its derivative f?'', we're to think ``Which function F has as its derivative this function f?''.
Memory serves us well in this process: if you've encountered a lot of functions and their derivatives in your days, you may well recognize an antiderivative from a given function. But one trick we may make use of is to recognize composite antiderivatives, from the chain rule.
Also in this section we find that we can use symmetry intelligently to integrate. Thinking of integrals as signed areas (sometimes positive, sometimes negative), any time we can make these areas ``balance out'' we should take advantage of it.