- cross-section: an intersection of a solid with a plane, which gives rise to an area. We then multiply these areas times a thin depth, to give rise to a volume.
-
volume: Let S be a solid that lies between x=a and x=b. If the
cross-sectional area of S in the plane
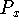, through x and perpendicular
to the x-axis, is A(x), where A is a continuous function, then the volume
of S is
-
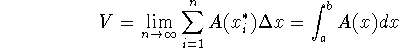
solids of revolution: solids obtained by revolving a region about a
line.
For a solid of revolution, the trick is to compute the radius r(x) (or, sometimes to ``confuse you'', r(y)), and rove over the appropriate axis.
This is a step up from computing areas: we're now computing volumes, by adding up little chunks of volume in the form A(x)dx (area times depth). The conceptual idea is the same, obviously, but we're in higher dimension.