-
Force: informally, a push or pull on an object. The force of gravity is
constantly forcing us to the floor (but the floor exerts an equal and opposite
force, which means that our velocity doesn't change - until the floor is pulled
out from underneath us!
Remember Newton's law: F=ma - force equals mass times acceleration. This important relationship is the source of many differential equations, which physicists have solved to explain how to put rockets on the moon, etc. [Remember that differential equations are those relating a function to its derivatives.]
The English units of force are pounds (which we often confuse with kilograms, which are a unit of mass). Hence weight is a measurement of force (which is why those people who got to the moon didn't have the weight on the moon that they did on the Earth - because the moon's acceleration due to gravity is not as strong as the Earth's). The astronauts had constant mass (their kilogram measurements would have been the same), but their weights were different on the Earth and on the moon.
The metric unit of force is the newton, named after the fig newton.
-
Work:
Now if we want to exert a force, it requires energy to do so. To push a box
across the floor, we exert energy. This energy we call work. Work is
defined as

(Work equals force times distance (or displacement)). This formula works great if the force is constant: we just multiply the force by the distance over which it's applied, and we have our work. But sometimes the force is a function of distance, and then we have to use the integral definition of work:
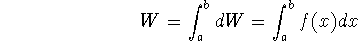
where a is the point at which we start applying the force, b is the point at which we stop, and we add up all the little bitsy dW=f(x)dx work chunks to get the total work W.
The unit of work is the foot-pound in English units, or the Joule (= newton-meter) in metric units (
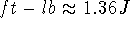 ).
).
-
Hooke's law: the force required to maintain a spring stretched x units
beyond its natural length is proportional to x:

where k>0 (called the spring constant). This law holds pretty well unless we stretch the spring so far that it's deformed.
This section illustrates the application of integrals to the definition of work, and gives us some examples of how to compute work in some relatively complex situations.
In particular, we see some spring problems, which require the use of Hooke's law. Hooke's law says that the force is proportional to the displacement from the equilibrium position of a spring.