-
one-to-one function: A function f is called a one-to-one function if
it never takes on the same value twice; that is,
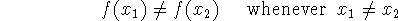
This means that each point in the range has a unique pre-image (element of the domain). Alternatively (and sometimes more usefully),
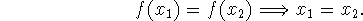
-
inverse function: Let f be a one-to-one function with domain A and
range B. Then its inverse function
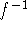 has domain B and range A and
is defined by
has domain B and range A and
is defined by
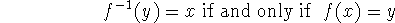
for any y in B.
-
If f is a one-to-one function defined on an interval, then its inverse
function
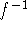 is also continuous. Because the graph of
is also continuous. Because the graph of 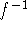 is simply
the mirror reflection of the graph of f, the continuity of f is also
reflected in the mirror.
is simply
the mirror reflection of the graph of f, the continuity of f is also
reflected in the mirror. -
If f is a one-to-one differentiable function with inverse function
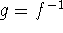 and
and 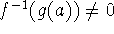 , then the inverse function is differentiable at a,
and
, then the inverse function is differentiable at a,
and

- Horizontal line test: A function is one-to-one if and only if no horizontal line intersects its graph more than once. This is of course akin to the vertical line test. It simply says that a graph could represent a function either of x as a function of y, or y as a function of x.
-
domain of
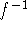 = range of f; range of
= range of f; range of 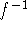 = domain of f.
We can think of these two functions as just ways of passing back and forth
between two sets.
= domain of f.
We can think of these two functions as just ways of passing back and forth
between two sets. -
Caution: do not mistake the -1 in
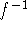 for an exponent:
for an exponent: 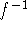 does
not mean
does
not mean 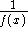 .
. -
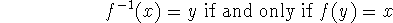
-
Cancellation equations:
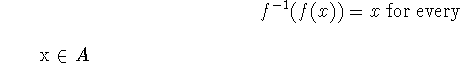
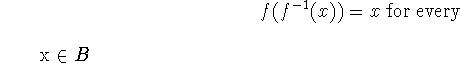
-
Method for finding the inverse of a function:
- Write y=f(x).
- Solve this equation for x in terms of y (if possible).
-
To express
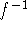 as a function of x, interchange the roles of x and y:
that is, write the resulting equation as
as a function of x, interchange the roles of x and y:
that is, write the resulting equation as 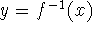 .
.
-
The graph of
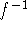 is obtained by reflecting the graph of f about the line
y=x.
is obtained by reflecting the graph of f about the line
y=x. -
Functions that are not one-to-one can be made so by restricting the domain. For
example,
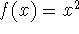 is not one-to-one (since
is not one-to-one (since 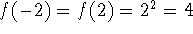 , but we can
restrict its domain to positive values of x and then write the inverse as
, but we can
restrict its domain to positive values of x and then write the inverse as
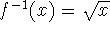 .
.
In this section we introduce the inverse function, which is the mirror
image of f about the line y=x. Hence, properties of ![]() are also
mirror reflections of those properties of f. It's easy to graph
are also
mirror reflections of those properties of f. It's easy to graph ![]() , for
example, once we have the graph of f, and properties of continuity and
differentiability are also easy to deduce. Even asymptotes are reflected! It's
even easy to compute slopes at a point on the inverse function if we know the
derivative of the function f.
, for
example, once we have the graph of f, and properties of continuity and
differentiability are also easy to deduce. Even asymptotes are reflected! It's
even easy to compute slopes at a point on the inverse function if we know the
derivative of the function f.
One can think of f and ![]() as ways of passing between two sets
(the domain and range of f, which are the range and domain of
as ways of passing between two sets
(the domain and range of f, which are the range and domain of ![]() ). A
secret code is an example of a function and its inverse: if I give you a secret
message, it's tranformed from an ordinary expression (the domain) by a function
and passed into a strange form (in the range). The secret agent on the other
end needs a method (the inverse function) that turns strange forms into
ordinary expressions.
). A
secret code is an example of a function and its inverse: if I give you a secret
message, it's tranformed from an ordinary expression (the domain) by a function
and passed into a strange form (in the range). The secret agent on the other
end needs a method (the inverse function) that turns strange forms into
ordinary expressions.