Section Summary: 7.4 - derivatives of logarithmic functions

1. Definitions
   • Logarithmic differentiation:
     1. Take logarithms of both sides of an equation y=f(x).
     2. Differentiate implicitly with respect to x.
     3. Solve the resulting equation for y'.

2. Theorems
   • The derivative of :

     

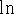     and using the chain rule, we have that

     

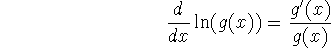
     Furthermore,

     

     (recall that, since 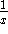is odd, its antiderivative - 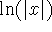- should be even! Hence,

     

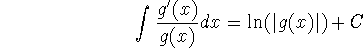
   • A straightforward application of the chain rule shows that

     

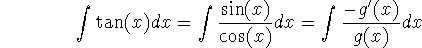
     so

     

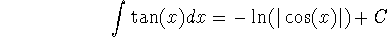
     Using the power law of logs, we have that

     

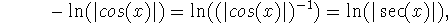
     so that

     

3. Properties/Tricks/Hints/Etc.
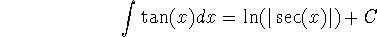
   • Two new formulations for the number e:

     

     and

     

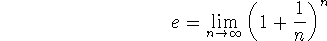
     Furthermore,

     

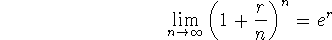
     which is so useful in compound interest problems: if we pay =r/n of the interest n times per year (compound interest), then let the number of payments times go to infinity (i.e., pay continuously), then in one year the account will be worth 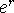times its initial value (rather than 1+r times, which is less).

4. Summary

   The derivative of the natural log function is easily obtained using a result from inverse functions: that

   

   Since the natural log is the the inverse of the exponential function with base e, we have that

   

   Simple! Furthermore, derivatives of compositions of functions with logarithms are easy to find. This is the mirror property of the simplicity of finding derivatives of compositions with exponential functions. It also gives rise to the idea of logarithmic differentiation, which uses the properties of logarithms to turn complicated quotient and product functions into simple functions whose derivatives can be found quickly and easily.

   Again, no need to worry about derivatives of other bases, since we can always replace an alien base with base e.

Problems to consider: pp. 443-444, #3, 4, 14, 20, 31, 36, 42, 62, 70, 82; on the board: 7, 11, 31, 32, 58, 67