Section 2.2 Worksheet:
Assigned problems: Exercises pp. 81-84, #4-16 even,
19, 30, 36
(due Thursday)
-
How do we read the expression

-
In expression (1) above, does x ever actually reach a?
-
How many ways can the limit

fail to exist?
-
Examples 4 and 5 (p. 76) illustrate some pitfalls of guessing limits. What are they?
-
Come up with at least 5 qualitatively different ways in which the graph of a function can have a vertical asymptote.
-
What conclusion can we draw from example 2, p. 74?
-
If
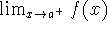 and
and 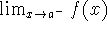 exist, does
exist, does
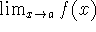 exist?
exist?
Notes:
-
The function
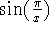 , whose graph appears on page 76, is a truly bizarre animal. When you encounter strange functions like this, make a note of them!
, whose graph appears on page 76, is a truly bizarre animal. When you encounter strange functions like this, make a note of them! -
Note the graph of
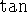 (p. 81). Like the graphs of
(p. 81). Like the graphs of  and
and 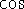 , you should be able to draw the graph of
, you should be able to draw the graph of 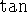 in your sleep.
in your sleep.
LONG ANDREW E
Fri Jan 24 11:00:00 EST 2003
![]()
![]()