Section 3.2 Worksheet:

Assigned problems: Exercises pp. 144-147, #3, 4, 5, 6, 10, 12, 14, 18, 21, 32 (due Monday, 2/10).

1. What does it mean for a function to be differentiable on an open interval?

2. There is one theorem in this section. What does it tell us? Can you follow the proof?

3. Describe at least three ways in which a function can fail to be differentiable at a point.

4. Are all continuous functions differentiable? If so, explain; if not, give a counter-example.

5. Make sure that you read the historical note on page 141. Name something that stands out to you about Leibniz's life.

6. How many different notations are presented for the derivative function? What are they?

7. Carefully examine Figure 2, p. 137, and make sure that you are clear on how the sign of the derivative is reflected in the curve of the function itself. What features in the graph of f indicate that the derivative function has a root?

Notes:

1. Figure 3, p. 138, really bugs the heck out of me: 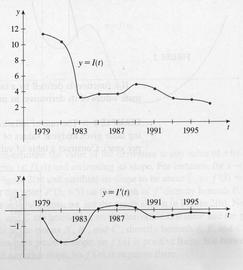It illustrates the problem of
   1. connecting tabular data with smooth curves, and
   2. approximating derivatives for tabular data.
   Given the smooth function which interpolates the given data, why do I object so strongly to the derivative shown below it?