Section 3.5 Worksheet:
Assigned problems: Exercises pp. 175-177, #4, 10, 13,
24, 26, 31, 35, 40, 46 (due Wednesday, 2/12).
-
Have a look at Appendix D. Are you familiar with everything therein? Learn to
use the ``tExpand'' command on your calculator (from the Algebra, then Trig
menus) to get expansions such as
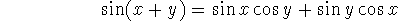
-
Suppose that you know that the derivative of the sine function is the cosine
function. How can you deduce the derivative of the cosine function using
Figure 1, p. 170, and horizontal shifts?
-
How could you give a graphical demonstration of the fact that

-
What trick is used in Example 4. p. 174, to find the limit?
Notes:
-
Note the use of the conjugate to prove that
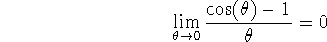
-
Note the use of the squeeze theorem to prove that

-
Again, for trigonometric functions make sure that you are using radians (and
not degrees) in your calculator. It makes a big difference!
-
Your author seems to think that you are going to memorize the derivatives of
the function in the table on page 173. I've only memorized two of them (the
derivatives of sin and cos), and don't expect you to do more than that. It's
easy to derive the derivatives of the others using the quotient rule. Some
people think that mathematicians like to memorize things; I like mathematics
because I have to memorize very little - the rest I can derive!
LONG ANDREW E
Tue Feb 4 12:10:59 EST 2003
![]()
![]()
![]()
![]()
![]()
![]()