Section 7.4 Worksheet:

Assigned problems: Exercises pp. 443-444, #3, 4, 14, 20, 31, 36, 42, 62, 70, 82 (due Thursday, 4/24).

1. Why would one want to use logarithmic differentiation? What advantage (if any!) does it offer?

2. Why is an antiderivative of 1/x equal to 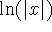, rather than simply ?

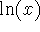3. This section contains two new ``definitions'' of the number e: what are they?

4. How can you use the fact that the natural log is the inverse function of 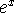to find the derivative of the log function, ?

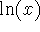Notes:

1. Interesting (and mysterious) connection: the derivative of a log is a rational function! This is the ``missing power'': the power rule works for all exponents but -1. An antiderivative of 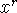is 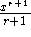for all r but r=-1.

2. Again, no need to worry about bases for logarithms other than base e, since it's easy to change from one to another.