Test 2: Concept Review
-
Interpretation of the derivative function as the slope of a graph at any point.
Definition of the derivative function as a limit. Differentiability implies
continuity (smoothness implies connectedness). Ways in which a function may
fail to be differentiable.
-
Special derivatives (e.g. derivatives of a constant, f(x)=x).
Differentiation Rules: Sum, difference, product, quotient, constant multiple,
power.
-
Applications of the derivative (e.g. biology, physics, chemistry, economics) as
an instantaneous rate of change. How to set up story problems - draw a picture!
-
Derivatives of trig functions (especially sine and cosine); definition of the
other trig functions (e.g. secant); how to derive the derivatives of the other
trig functions from those two principal trig function (quotient rule!).
Special limits (e.g.
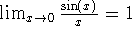 ).
). -
The Chain rule: how to use it; how to represent it. ``The derivative of f
of stuff is equal to f prime of stuff times stuff prime.'' Remember that this
is a very mechanical process: identify the composition, find the two
derivatives, and apply the rule!
-
Higher derivatives; physical meaning of the higher derivatives (e.g. velocity,
acceleration, jerk).
-
Related rates (drawing a good picture, establishing well-named variables and
constants, finding the data, finding an equation relating the variables, and
``differentiating the equation'' to relate the rates).
-
Extrema: absolute maxima and minima, local maxima and minima
-
Extreme Value Theorem (a continuous function has absolute extrema on a
closed interval)
-
The closed interval method (finding absolute extrema using critical points and endpoints)
-
Fermat's theorem (if f is differentiable and there's an extremum at c, f'(c)=0)
-
The Mean Value Theorem (with Rolle's theorem as a special case): the
instantaneous rate of change matches an average rate of change somewhere.
-
How derivatives affect the shape of a graph
-
Increasing/decreasing test; first and second derivative tests
-
Concavity test (concave up - bowl - and concave down - umbrella), and
inflection points
In the meantime, don't forget the basics from the first test: how to find
domains of functions, the definition of derivatives as limits, etc. While the
focus will be on the new material, you will still be expected to be able to use
the old stuff!
LONG ANDREW E
Wed Mar 5 11:49:35 EST 2003