Test 3: Concept Review

Section 4.4: Limits at infinity

• Horizontal asymptotes - function becomes constant, derivative heads for zero
• Three cases for rational functions:
  1. 
  2. 
  3. 

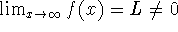
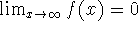
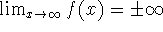
Section 4.5: summary of curve sketching

• DISAILCS - a silly acronym for the 8 steps of curve sketching: Domain-Intersepts-Symmetry-Asymptotes-Intervals-Local extrema-Concavity-Sketch
• slant asymptotes (and which rational functions lead to them) - function tends to a linear function, with constant derivative.

Section 4.7: Optimization problem

• Make sure that you start with a good picture, which helps us both understand what you understand!
• I like the UPCE (``oopsie!'') method: Understand, Plan, Carry out, Evaluate.
• Check endpoints, as well as critical points, for extrema.
• Use your mathematical wealth! Pythagoras, trig, etc.

Section 4.10: Antiderivatives

• Finding general anti-derivatives by thinking backwards (don't forget your C!)
• Finding specific anti-derivatives
• Differential equations - what are they? JFF (just for fun!)
• Direction Fields - what are they? (just for fun!)

Section 5.1: Areas and Distances

• Area as a limit of rectangles becoming very thin.
• sample points ,
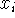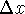
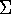• (sigma) notation
• left and right endpoint rectangle approximations
• the ``dirt'' formula (distance = rate time)

Section 5.2: the definite integral

• Definition of a definite integral
• Riemann sum
• vocabulary (integrand, integral sign, differential, limits of integration)
• midpoint rule
• trapezoidal rule (actually equivalent to the average of left and right rectangle rules)
• properties of the integral (1-8, pp. 331-333)

Section 5.3: Fundamental Theorem of calculus

• Fundamental theorem of calculus
• graphing anti-derivatives from integrals

Section 5.4: Indefinite integrals

• Indefinite integrals
• Difference between definite and indefinite integrals
• Watch the continuity of the integrand (e.g. top of p. 348)
• Total Change theorem

Section 5.5: Substitution

• Substitution rule (using the chain rule in reverse - look for a function inside a composition and its derivative)
• Difference between substitution for indefinite integrals and definite integrals (in which the limits of integration must be carefully handled!).
• Using symmetry to calculate integrals (odd functions over symmetric intervals are easy!)

Section 6.1: Areas between curves

• Areas between curves (making sure which function is on top of the other!)
• Integrating along the y-axis as well as the x-axis

Don't forget the basics from previous tests. While the focus will be on the new material, you will still be expected to be able to use the old!