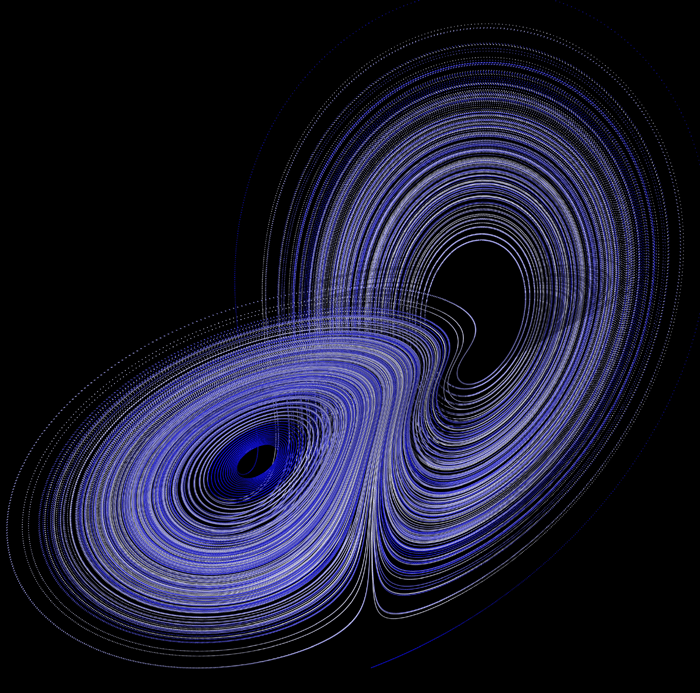
The Lorenz Attractor in 3DImages by Paul BourkeApril 1997
PovRay code by Marcus Fritzsch
|

|
The Lorenz Attractor in 3DImages by Paul BourkeApril 1997
PovRay code by Marcus Fritzsch
|

|
The so called "lorenz attractor" was first studied by Ed N. Lorenz, a meterologist, around 1963. It was derived from a simplified model of convention in the earths atmosphere. It also arises naturally in models of lasers and dynamos. The system is most commonly expressed as 3 coupled non-linear differential equations.
dy / dt = x (b - z) - y
dz / dt = xy - c z
One commonly used set of constants is a = 10, b = 28, c = 8 / 3. Another is a = 28, b = 46.92, c = 4. "a" is sometimes known as the Prandtl number and "b" the Rayleigh number.
The series does not form limit cyles nor does it ever reach a steady state. Instead it is an example of deterministic chaos. As with other chaotic systems the Lorenz system is sensitive to the initial conditions, two initial states no matter how close will diverge, usually sooner rather than later.
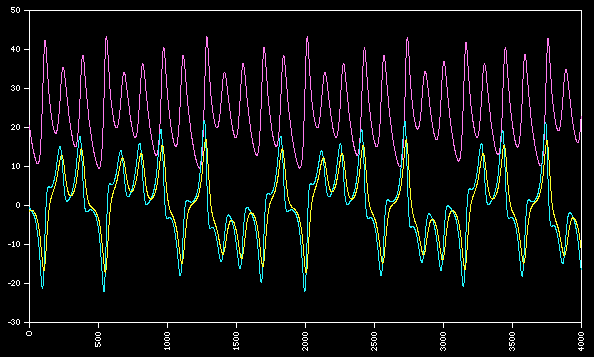
Typical traces of each coordinate are shown below
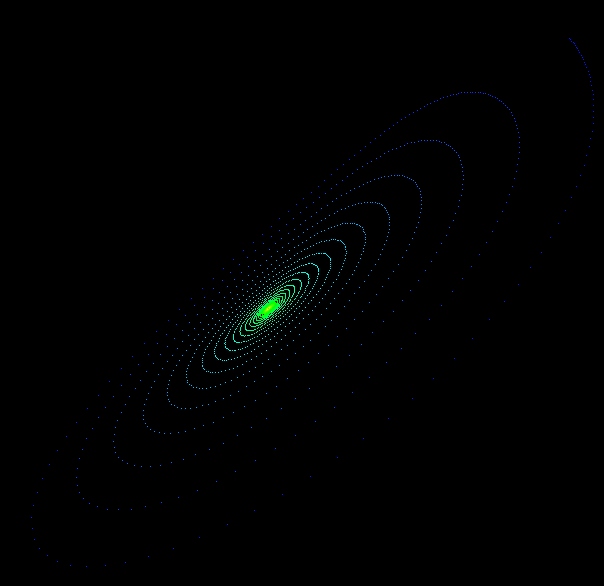
While the equations look simple enough they lead to wonderous trajectories, some examples of which are illustrated below.


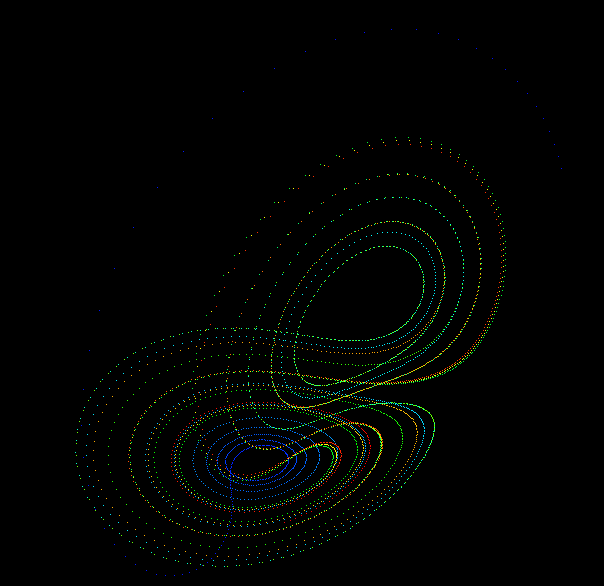
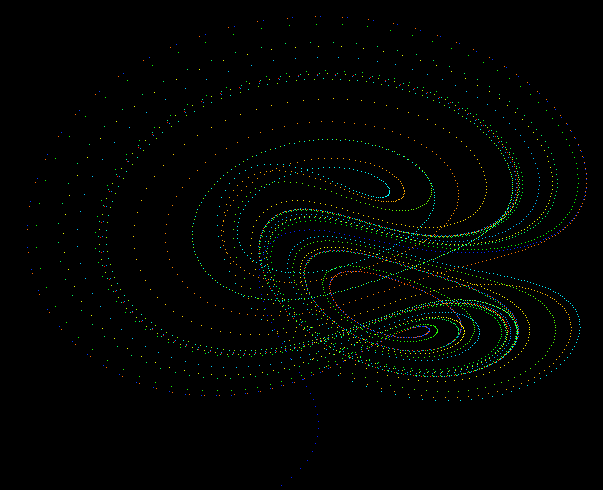
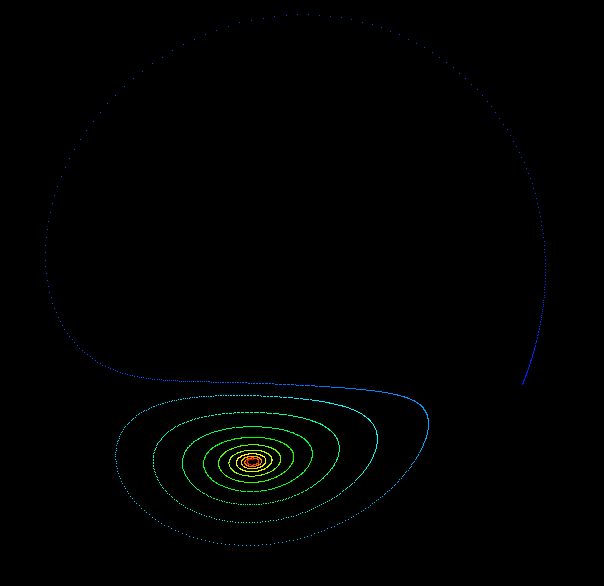
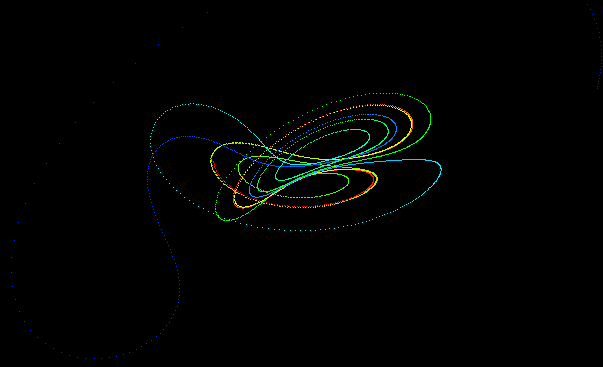
PovRay 3.5 macro by Marcus Fritzsch
// N = number iterations
// h, a, b, c: initial parameters
// x0, y0, z0: start-location
// rad = radius of the spheres that trace the attractor
#macro lorenz(h, a, b, c, x0, y0, z0, N, rad)
// use it like:
// lorenz(0.001099, 10, 28, 8/3, 0.0001, 0.0001, 0.0001, 350000, 0.04)
#local i = 0;
union {
#while (i < N)
#local x0 = x0 + h * a * (y0 - x0);
#local y0 = y0 + h * (x0 * (b - z0) - y0);
#local z0 = z0 + h * (x0 * y0 - c * z0);
#if (i > 100)
sphere {
<x0,y0,z0>, rad
pigment { color rgb <i/N,i/N,1> }
}
#end
#local i = i + 1;
#end
}
#end
|
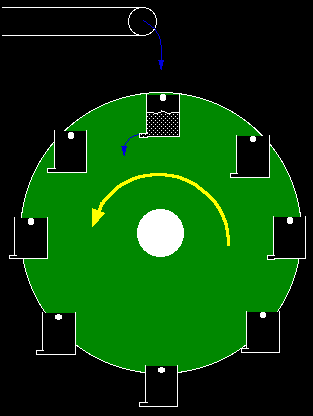
A physical model simulating the Lorenz equations has been attributed
to Willem Malkus and Lou Howard around 1970.
It consists of leaking cups on the rim of a larger wheel as shown in
the diagram on the right. Liquid flows from the pipe at the top, each
cup leaks from the bottom.
|
|
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#define N 10000
int main(int argc,char **argv)
{
int i=0;
double x0,y0,z0,x1,y1,z1;
double h = 0.01;
double a = 10.0;
double b = 28.0;
double c = 8.0 / 3.0;
x0 = 0.1;
y0 = 0;
z0 = 0;
for (i=0;i<N;i++) {
x1 = x0 + h * a * (y0 - x0);
y1 = y0 + h * (x0 * (b - z0) - y0);
z1 = z0 + h * (x0 * y0 - c * z0);
x0 = x1;
y0 = y1;
z0 = z1;
if (i > 100)
printf("%d %g %g %g\n",i,x0,y0,z0);
}
}

PovRay rendering by Marcus Fritzsch