The Shape of Space
Have cosmologists glimpsed signs that the universe is bounded?
Erica Klarreich
Gaze
deep into the night sky, and space appears to extend infinitely far in
all directions. Given such a view, it's mind-boggling to think that
space might be bounded. Yet, just as the flat-seeming Earth is in fact
a sphere, infinite-seeming space may curve in on itself to close up
into a compact shape. Recently, the debate over the shape of space took
some new twists. In the Oct. 9 Nature, a team of
mathematicians and astrophysicists proposed an exciting idea. The
universe may have a particular finite shape, modeled on a 12-sided
geometric object known as a dodecahedron, they propose. The same week,
a second group of scientists announced findings that may refute that
proposal. Both groups have based their analyses on first-year data from
NASA's Wilkinson Microwave Anisotropy Probe (WMAP), which in February
produced a snapshot of temperature waves shortly after the Big Bang
(SN: 2/15/03, p. 99: http://www.sciencenews.org/20030215/fob1.asp).
These waves produced a puzzle: One of the longest wavelengths, known as
the quadrupole, is less powerful than expected. This is like saying, in
an analogy with sound waves, that the universe doesn't play low notes. To many cosmologists, the reduced quadrupole is a hint that
the universe may be finite. In an infinite universe, all wavelengths
should be equally abundant, whereas in a finite universe, waves can
never be longer than the universe itself. By analogy, "you don't get really long waves in a bathtub
because the waves can't be bigger than the bathtub is long," says
Jeffrey Weeks, a freelance geometer based in Canton, N.Y., who is one
of the authors of the Nature paper.
Complex soccer ball
Weeks and his coauthors report that a shape called the Poincare
dodecahedral space is a good fit for both the quadrupole data and
estimates of the universe's curvature.  | HALL
OF MIRRORS. In the dodecahedral model of the universe, each pentagonal
face is theoretically glued to the opposite face. In such a universe,
if you look straight through one of the faces, you see what looks like
a new dodecahedron but is really the original dodecahedron seen from a
new vantage point.
Weeks |
The Poincare dodecahedral space is formed by gluing together opposite
faces of a slightly curved dodecahedron—a soccer-ball-like shape with
12 pentagonal sides. Such a gluing is impossible to carry out
physically within ordinary three-dimensional space. However, by keeping
track of which faces are theoretically glued, scientists can measure
the physical attributes of such a space. If the universe had this shape, a traveler who crossed through
one of the pentagonal faces would instantly reappear at a face on the
opposite side of the dodecahedron. Video game characters make such
treks in two dimensions when they vanish from one side of the screen
and reappear at the other. In the dodecahedral universe, a trip across
the solid would span many billions of light-years. Weeks and his collaborators were drawn to study the
dodecahedron because recent observations of the universe's cosmic
microwave background radiation have suggested that the universe either
is flat or has slightly positive curvature, such as a sphere does. This
estimate makes many of the possible shapes for the universe unlikely.
The few more-likely candidates include the dodecahedron and a shape
called the three-torus, made by gluing opposite sides of a box. Preliminary examinations of various kinds of three-torus—made
from boxes of different shapes and sizes—have yielded no shape that
fits the quadrupole data well. The dodecahedron model, however, appears
to match data on both the quadrupole and the next-longest wavelength,
called the octopole. Not so fast
The Poincare dodecahedron's apparent match with the quadrupole
data and the curvature measurement is "intriguing," says David Spergel,
an astrophysicist at Princeton University and a member of the WMAP
team. However, at a cosmology conference in Cleveland on the day after
the Nature paper appeared, Spergel reported findings that he says undermine the dodecahedron model.
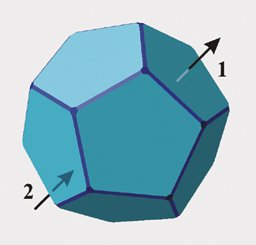 | SPACE
TREK. In dodecahedral space, if you journey across one pentagonal face
(1), you instantly reappear through the opposite face (2), on the other
side of the universe.
Weeks |
Spergel and his collaborators examined whether the dodecahedron
satisfies a criterion called the circle test. This criterion rests on
the observation that, because we can see equally far in all directions,
the boundary of our visible universe is an enormous sphere. Think of our visible universe as a bubble at the center of the
dodecahedral model. If the bubble were much smaller than the
dodecahedron, we would see nothing of the pentagonal faces. If the
bubble were to grow, it would eventually touch each pentagonal face at
a single point at the center. If the bubble were to grow a tiny bit
further, it would cross each face, intersecting it in a circle. According to the model in the Nature paper, the
dodecahedral universe is just the right size for the bubble to
intersect the pentagonal faces in circles. Because each of the 12
pentagonal faces is glued to the opposite face, each circle should
match an identical circle on the opposite pentagon. Therefore, the sky
should contain six pairs of matching circles on which all the physical
data, including the temperature waves in the WMAP data, are identical. Spergel and his collaborators have been combing the WMAP data
looking for such circle pairs. According to Spergel, the circles are
not there. Weeks agrees that the absence of matching circles would kill
the dodecahedron model. However, he says, it's possible that Spergel's
team missed the circles. Although in principle we should see identical
light coming from the matching circles in the sky, in reality, effects
such as noise obscure the circle pairs. If the noise is strong enough,
Weeks says, the circles might elude detection by the algorithm
Spergel's team used. The WMAP team has tested its algorithm on a simulated sky map
that factored in noise and other distortions, says Neil Cornish of
Montana State University in Bozeman, one of Spergel's collaborators.
According to those simulations, if circles are in the sky, there is
less than a 1 percent chance that the algorithm would miss them. However, the team carried out its test simulations in a
three-torus model rather than a dodecahedral model. It's not clear
whether the 1-percent-error estimate would carry over to the
dodecahedron, Weeks says. The circle search team plans to run its simulations on the
dodecahedral shape. "We're going to be able to make extremely strong
statements about their model," Cornish says. "It's such a dramatic
claim that it's worth going that extra mile to test it." However, he does not expect the simulations to validate the
dodecahedron model. "I really think there isn't any room left," he
says. Testing, testing
Until Spergel, Cornish, and their collaborators have performed
simulations on the dodecahedron and cosmologists have had a chance to
scrutinize the work, it's premature to agree or disagree with the
team's findings, Weeks says. "The recent history of cosmic topology is
littered with examples of people claiming to rule out various
possibilities, only to find later that their analysis had flaws," he
notes. At this point, he says, both the dodecahedron model and the
evidence against it should be considered with caution. If the dodecahedron is ruled out, "it will be a
disappointment," Weeks says. "It fits the data really well, and there
aren't a lot of back-up candidates to go." Among the plausible shapes
that remain to be tested is a three-torus made out of a slanted box. In an ambitious project, Spergel, Cornish, and their
colleagues are scanning the sky for any evidence of circle pairs that
would indicate these or other possible shapes. That wider search should
be completed soon, Cornish says. "What's nice is that we don't need to launch another satellite
to test [the models]," says Max Tegmark, a cosmologist at the
University of Pennsylvania in Philadelphia. "The answer is there in the
data and just needs to be ferreted out." If the dodecahedron model turns out to be incorrect, the question of why the universe doesn't play low notes will remain.
"We don't know whether it's a fluke, a compact universe, or some
other cosmological effect," says Charles Bennett of NASA's Goddard
Space Flight Center in Greenbelt, Md., who is the director of the WMAP
project. "That's the exciting part." ****************
If you have a comment on this article that you would like considered for publication in Science News, send it to editors@sciencenews.org. Please include your name and location.

References: Cornish, N.J.,
D.N. Spergel, G.D. Starkman, and E. Komatsu. Preprint. Constraining the
topology of the universe. Abstract available at http://xxx.lanl.gov/abs/astro-ph/0310233.
Ellis, G.F.R. 2003. The shape of the universe. Nature 425(Oct. 9):566-567.
Luminet, J.-P., J.R. Weeks, et al. 2003.
Dodecahedral space topology as an explanation for weak wide-angle
temperature correlations in the cosmic microwave background. Nature 425(Oct. 9):593-595. Abstract available at http://dx.doi.org/10.1038/nature01944. Further Readings: Cowen, R. 2003. Cosmic revelations: Satellite homes in on the infant universe. Science News 163(Feb. 15):99-100. Available at http://www.sciencenews.org/20030215/fob1.asp.
______. 1998. Cosmologists in Flatland. Science News 153(Feb. 28):139-141.
Peterson, I. 1998. Circles in the sky. Science News 153(Feb. 21):123-125. Available at http://www.sciencenews.org/sn_arc98/2_21_98/bob1.htm.
Information about the Wilkinson Microwave Anisotropy Probe can be found at http://map.gsfc.nasa.gov/. Sources: Charles L. Bennett
Laboratory for Astronomy and Solar Physics (LASP)
Code 685, Infrared Astrophysics Branch
NASA Goddard Space Flight Center
Greenbelt, MD 20771
Web site: http://lasp-nts1.gsfc.nasa.gov/irbranch/Bennett.html
Neil J. Cornish
Department of Physics
Montana State University
Bozeman, MT 59717
David N. Spergel
Department of Astrophysical Science
Princeton University
Princeton, NJ 08544
Max Tegmark
Department of Physics
University of Pennsylvania
Philadelphia, PA 19104
Web site: http://www.hep.upenn.edu/~max/main.html
Jeffrey R. Weeks
15 Farmer Street
Canton, NY 13617-1120
|