- Theorem 1: consider the limit as x approaches c:
sums, differences, product, and quotients behave exactly as hoped:
The limit of the NOSE of two functions is the NOSE of the two limits.
(replace the word NOSE in the statement above with any of the other vocab words).
- Notes:
- The Theorem requires that the limits exist separately for the two functions at x=c.
- We have to be a little careful with the quotient, just to make sure that the limit of the denominator function is not zero....)
- The "constant multiple law" is deduced from the product law and with Theorem 1 from 2.2: that the limit of a constant function is the constant itself.
- The theorem also applies to one-sided limits.
- Examples:
- #10, p. 62
- #18, p. 62
- #24, p. 63
- Questions over the Directed reading handout, Section 2.3 (html) (pdf)?
- Continuity:
- The limit at x=c exists and is equal to f(c)
- When a function is continuous at for all values in its domain, we say simply that it is a continuous function.
- Discontinuity: three main types:
- jump
- removable
- infinite
We define one-sided continuity, which helps resolve some of these discontinuities. Where does the function fail to be continuous, but demonstrate continuity from the left or the right?
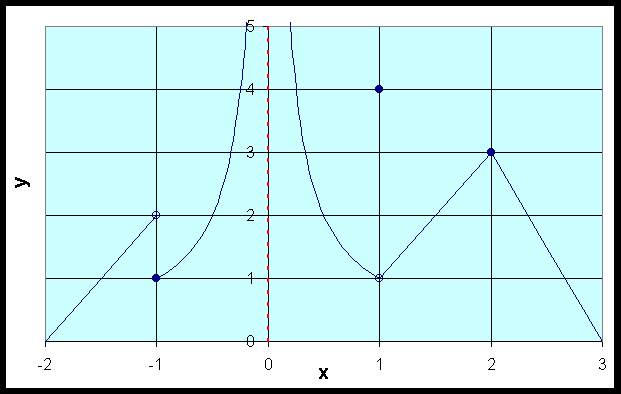
- Theorems:
- Theorem 1: concerns continuity at x=c, for
sums, differences, products, and quotients:
If two functions are continuous at x=c, then the NOSE of the two functions is continuous there.
(replace the word NOSE in the statement above with any of the other vocab words).
- Theorem 2: All polynomials and rational functions are continuous on their domains.
- Theorem 3: sin, cos, exponential functions, and power functions are continuous on their domains.
- Theorem 4: compositions: if
g is continuous at x
and
f is continuous at g(x)
then
f(g(x)) is continuous at x.
- Theorem 1: concerns continuity at x=c, for
- Notes:
- The usual problem with the quotient, just to make sure that the limit of the denominator function is not zero....)
- To evaluate limits of continuous functions is easy: simply substitute the value of c for x in the formula for f(x) (called the substitution method)
- Examples:
- #6, p. 71
- #14, p. 71
- #20, p. 71
- #56-70 even, p. 73
- #77, p. 73
- I learned something about our atmosphere: Figure 13
- Questions over the Directed reading handout, Section 2.4 (html) (pdf)?