- There's really nothing too new here: just instead of calculating the area between a curve (the graph of the function given by f(x)) and the x-axis (the graph of the function g(x)=0), we compute the area between two arbitrary curves, given by the graphs of f(x) and g(x):
- If we're computing area -- real, honest-to-goodness, positive area -- then we have to make sure that we know which function's graph is "on top". In effect, we want to compute
- One of the interesting twists in this section is integrating along the
y-axis. Actually, we could just swap variables x and y,
and we'd be back to integrating along the x-axis, but we should be more
dexterous than that...
- Examples:
- #33, p. 307
- #43, p. 307
- The hardest job is often visualizing what's going on. Then the problem
becomes figuring out the little chunks of stuff that one wants to add up to get
the whole quantity of stuff. Here are some classic examples:
- Volumes:

- Population density:

- Flow rate:
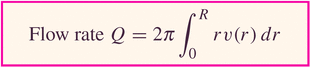
- Average Value:
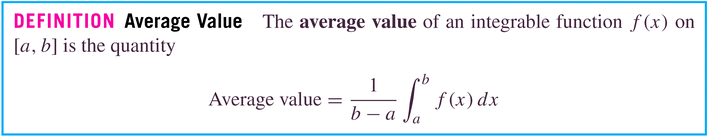

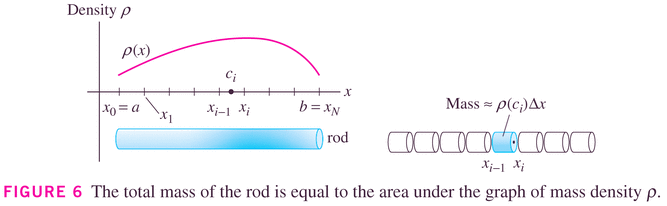
- Mass density:
- Examples:
- #2, p. 317
- #4abc, p. 317
- #6, p. 317
- #26, p. 318
- #30, p. 319
- #33, p. 319
- #53, p. 319