Chernoff Faces

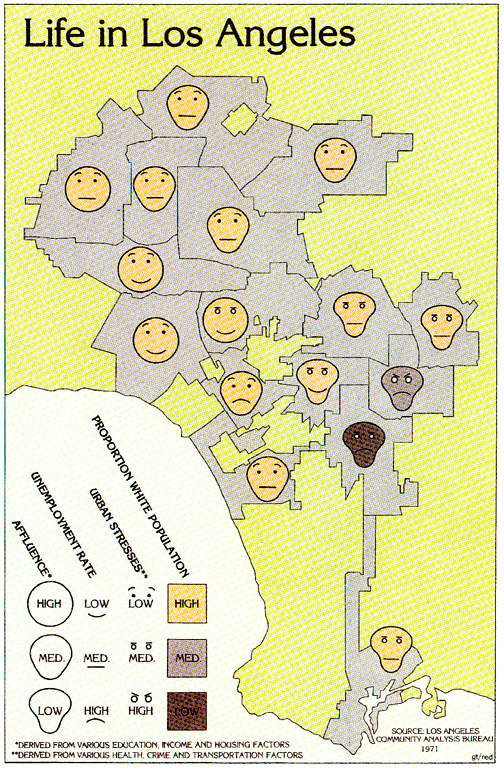
Chernoff Faces Herman Chernoff, "The use of faces to represent points in k-dimensional space graphically," J. Am. Stat. Assoc., v68, 361-368 (1973).

In 1973, Herman Chernoff introduced a visualization technique to illustrate trends in multidimensional data. His Chernoff Faces were especially effective because they related the data to facial features, something which we are used to differentiating between. Different data dimensions were mapped to different facial features, for example the face width, the level of the ears, the radius of the ears, the length or curvature of the mouth, the length of the nose, etc.

They use facial features to represent trends in the values of the data, not the specific values themselves. While this is clearly a limitation, knowledge of the trends in the data could help to determine which sections of the data were of particular interest.

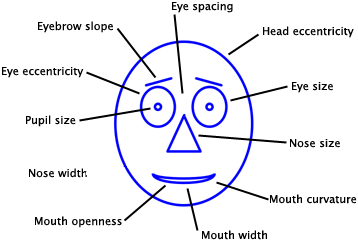
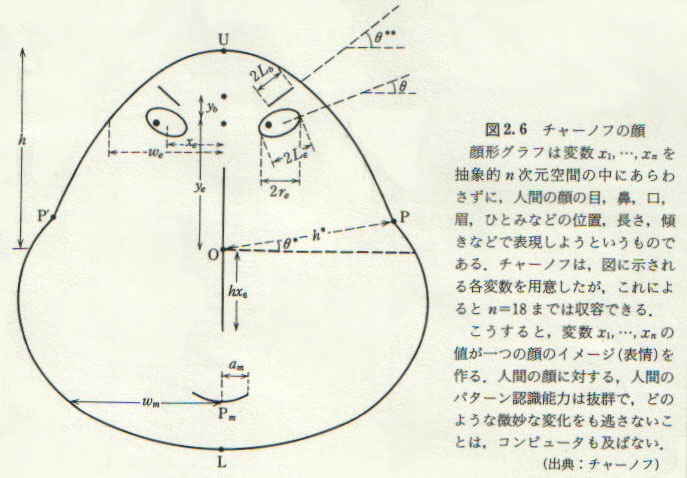
Here, the faces are described by 10 facial characteristic parameters: 1. head eccentricity, 2. eye eccentricity, 3. pupil size, 4. eyebrow slant, 5. nose size, 6. mouth shape, 7. eye spacing, 8. eye size, 9. mouth length, and 10. degree of mouth opening. Each parameter is represented by a number between 0 and 1.

All 0.

All 0.5.

All 1.

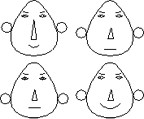
Randomly selected parameters.
Change face.

Animation with random parameters.

Applet by John Wiseman

The power of Chernoff face is its high condensation of data and its interesting way of presentation. Scott (1992) found that repetitious viewing of large tables of data is tedious, but Chernoff faces can significantly improve data digestion. A major drawback of Chernoff faces is that the subjective assignment of facial expressions to variables affects on the shape of the face. Chernoff and Rizvi (1975) found that the permutations of the assignment of features caused an error rate of as high as 25 for the task of classifying faces into groups. It means that classifying two faces as "fairly similar" is greatly influenced by the assignment of variables to specific features. Furthermore, some researchers such as Flury and Riwdwyl (1981), and Turner and Tidmore (1980) criticized that the symmetrical feature of Chernoff faces is redundant. Like the "star graph" or "radar plot", the power of showing multiple relationships in Chernoff faces are limited in a still mode. With the advance of computer technology, animated Chernoff faces may be worthy to experiment with. [Yu]

References

Scott, D. W. (1992). Multivariate density estimation: Theory, practice, and visualization. New York: John, Wiley & Sons.
Chernoff, H., & Rizvi, M. H. (1975). Effect on classification error or random permutations of features in representing multivariate data by faces. Journal of American Statistical Association, 70, 548-554.
Flury, B., & Riedwyl. H. (1981). Graphical representation of multivariate data by means of asymmetrical faces, Journal of American Statistical Association, 76, 757-765.
Turner, D. W., & Tidmore, F. E. (1980). FACES-A FORTRAN program for generating Chernoff-type faces on a line printer. American Statisticians, 34, 187.

Design

Example