- Sorry, I've not yet finished grading the exam. I hope to have it
done by tomorrow.
But I'm drawing some conclusions already (detail when I hand back the tests).
- Section 8.1 homework is due today - on-line and hand-in
components.
- First of all, the big picture: integration by parts is just the
product rule backwards. This integration technique, like all
integration techniques, is really just a differentiation technique in
reverse.
Example: Exercise #2, p. 428
- Integration by parts may need to be carried out multiple times:
sometimes the idea is to simplify the integral each time, until a
really simple one arises allowing us to calculate the final solution
(e.g. Example 4, p. 425). Sometimes it's something of a trick: we
compute the integral multiple times in order to return to the original
integral, allowing us to solve an equation for the original integral
(e.g. Example 5, p. 426).
Example: Exercise #18, p. 428
- Suggested strategy:
- Choose u so that u' is simpler than u itself.
- Choose v' so that
can be evaluated.
- Sometimes v'=1 is a good choice.
Example: Exercise #25, p. 428
- Of course, all this works with definite integrals:
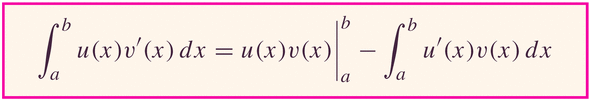
Example: Exercise #49, p. 428
- In this section we deal with integrals of two sorts: those whose limits of integration are infinite, and those with vertical asymptotes.
- Definition concerning the first type:
Here's an important example:


- The following figure illustrates the first type, and also the
second:

The integral exists over
But what can we say about the integral over (0,2]?

- There's a general rule for powers (it's easy to take the limits
and check):

Let's check in this case:

The case of p=1 is interesting, and we can use symmetry to see that it is so.
- There's a third component of this section which is interesting:
the idea of using bounding to deduce whether an integral
diverges or converges. For example, we can use comparison to
show that, in fact,

This one has infinite limits on both ends -- how do we handle that?
- We could use symmetry, of course; but more generally,
How would we use comparison? We find a function which is everywhere greater than the function but which has finite area. Can you think of a good candidate?

- We could use symmetry, of course; but more generally,
- Examples:
- #13, p. 464
- #12, p. 464
- #44, p. 465