Day 38 in MAT229

Today:

• Announcements:
  • Homework 11.4: grading #10, 20 (sorry, not done yet)

  • Homework 11.5: due today

  • Special Homework Assignment: p. 586, #46, 49; due Tuesday, 11/11

  • Reminder: The Sehnert Lecture is today!

• How are things going? What questions do you have?

• Last time: Dr. Krug provided some background material on differential equations:
  • First-order, Linear ODEs -- e.g.
  • First-order, Non-Linear ODEs -- e.g.

• I'd hoped that Jim Cushing, our Sehnert Lecturer, might be available to lecture today on some of the work that he's doing, but that was impossible.

  For example, Dr. Cushing studies "Bifurcations" -- when some aspect of the solution illustrates a qualitative change in response to a change in a parameter value (e.g. calculator example of solutions of the first-order, linear ODE above).

  In particular, he studies how changes in parameter values can lead to "chaos" -- informally,

  • "extremely complicated dynamics," or
  • "sensitive dependence on initial conditions".

  In lieu of his visit, I'd like to continue with 11.6, and demonstrate some of the applications of power series techniques to the solution of ODEs.

• Section 11.6
  • Let's use #44, p. 586 as our illustrative example -- an example of the first order, linear ODE.

    We are asked to refer to Theorem 1, section 7.4 in our solution.

  • Now, we can also consider Second-order linear ODEs, such as , and solve them via the power series solution method.
    • Let's consider
    • We need to give two initial conditions to completely specify the solution.
    • Consider and

      Can you think of a function that satisfies these conditions? (The general method of solving DEs!;)

    • Then let's do it the power series way....

  • Examples
    • Consider the non-linear, first-order ODE
      • What happens (that seems different) when we attempt to solve the DE using power series?
      • How could we solve this analytically w/o power series?

    • #47, p. 586

• Section 11.7: Taylor Series
  • We've basically seen all this material before: we're now just summarizing:
    
    is the Taylor Series expansion of f(x) centered at x=c. The special case of c=0 is called the Maclaurin series. The factorials in the denominator sweep up all the powers that pop down during the n differentiations.

    The coefficients are "designed" so that after n differentiations of the series, when we evaluate the series we pick off only the n^th derivative evaluated at x=c:

    

    

    We've seen that, because of the radius of convergence, the function may not be represented by a power series at some values of x (even as it's perfectly represented at other values of x).

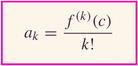
    If we can bound all derivatives of a function on an interval about x=c, then the Taylor series represents the function there:

    

    The expansion for the binomial series is a classic: it's another of the great achievements of Sir Isaac Newton, one of the founders of calculus:

    

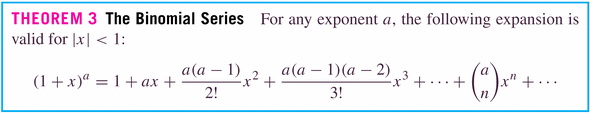
  • Examples:
    • #1, p. 596
    • #4, p. 596 (remember that there are several different ways to do these! You don't have to work from the definition....)