Day 41 in MAT229

Today:

• Announcements:
  • Return Homework 11.6: graded #11, 14

  • Special Section 11.6 assignment due today

  • Assignment for 11.7: To be handed in (due Monday, 11/17): pp. 596-599, #7, 14, 26, 32, 40, 47, 77, 78

• Section 11.7: Taylor Series
  • We've basically seen all this material before: we're now just summarizing:
    
    is the Taylor Series expansion of f(x) centered at x=c. The special case of c=0 is called the Maclaurin series. The factorials in the denominator sweep up all the powers that pop down during the n differentiations.

    The coefficients a_kare "designed" so that after k differentiations of the series, when we evaluate the series we pick off only the k^th derivative evaluated at x=c:

    

    

    We've seen that, because of the radius of convergence, the function may not be represented by a power series at some values of x (even as it's perfectly represented at other values of x).

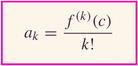
    If we can bound all derivatives of a function on an interval about x=c, then the Taylor series represents the function there:

    

    The expansion for the binomial series is a classic: it's another of the great achievements of Sir Isaac Newton, one of the founders of calculus:

    

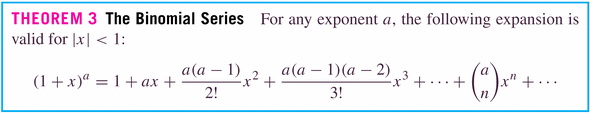
  • Examples:
    • #4, p. 596 (remember that there are several different ways to do these! You don't have to work from the definition....)
    • #1, p. 596
    • #21, p. 597
    • #33, p. 597
    • Conditional convergence is funny.... e.g. ln(2), using the series in Table 1, p. 596:

      The Taylor series for ln(1 + x) is x - x²/2 + x³/3 - x⁴/4 + .... For x = 1, we have ln 2 = 1 - 1/2 + 1/3 - 1/4 + ... .

      Let's rearrange the summation in the series for ln 2 and see what happens. Suppose we pull some negative terms forward to get 1 - 1/2 - 1/4 + 1/3 - 1/6 - 1/8 + 1/5 - 1/10 - 1/12 + 1/7 - ... . Each reciprocal of an odd integer is followed by two negative terms of reciprocals of even integers. In the n^th group of three terms, they are 1/(2n - 1) - 1/(4n - 2) - 1/4n or (1/2)[1/(2n - 1) - 1/2n]. Therefore, we have just half of each term in the series for ln 2. This series will converge to (1/2)ln 2 = 0.34657.

      From this source. Now that's bizarre! By just rearranging the terms, we can get it to converge to something else! That's because the convergence is only conditional. If it were absolute, then the order won't matter.

    • Now: knowing that, an observation about some important even and odd functions, starting with the function e^x.

• Section 12.1: parametric curves
  • Homework: To be handed in (due Tuesday, 11/18): pp. 611-615, #3, 12, 20, 30, 40, 52, 54, 55, 89

  • And now for something completely different....

    A good introduction to parametric curves is given by ballistics. If we shoot a bullet into the air with speed v horizontally, and we neglect all forces but gravity, then the bullet will trace out a parabola:

    

    Now how might we characterize the path of the bullet? The answer is a parametric curve, of the form C(t)=(x(t), y(t)).

    or
    If we wish, we can solve for t in the equation for x and use that to eliminate the parameter t from the equation for y, hence getting an equation for the parabola traced out:

    Orbits of planets in the heavens, movements of ants on a hill, a robotic arm in an assembly plant: all these are described by parametric curves.

  • A couple of famous examples involving the cycloid:
    
    • The Brachistochrone Problem (1696, solved by Newton in a single day after he heard the challenge)
    • The Tautochrone Problem (1673)

  • Parametrizing a line:
    

  • Parametrizing a circle:
    

• There are two distinctively different kinds of derivatives that we're going to have to consider here:
  • There are the time-derivatives, which give us the actual speeds of the "particles" as they zip along in time. For the bullet, the speed will be
    

  • There is the slope of the tangent line to the curve traced out by the particle, which one can obtain using the time-derivatives:
    

• One of the most important applications of parametric curves is in the Bezier curve section, p. 609. There are lots of important instances where we need to be able to design custom curves, and this is one of the most common ways of creating them. For example, you can use them to create your own "sigmac", using control points. (I had all my students create their own in numerical analysis.)

• Examples:
  • #11, p. 611
  • #14, p. 611
  • #19, p. 611
  • #22, p. 611
  • #50, p. 612