
In this section we consider an algorithm (Gaussian elimination with partial pivoting) for reducing a system of equations to reduced echelon form, which is unique and allows us to write the solution set of a linear system. The solution may contain free parameters, meaning that there are infinitely many solutions.
Definition: A rectangular matrix is in row echelon form if it has the following three properties:
Example:

Definition: A matrix in echelon form is in reduced row echelon form if it has the additional two properties:
Example: The matrix above in reduced row echelon form is
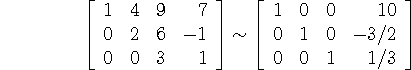
Theorem: Each matrix is row-equivalent to one and only one reduced row echelon matrix.
Example: The ![]() identity matrix
identity matrix ![]() :
:

Example: #2, p. 25
Note: The uniqueness of the reduced row echelon matrix implies that the positions of the leading non-zero entries are fixed in stone for a given matrix. These positions are known as pivot positions. A pivot column of a matrix is one that contains a pivot position.
This leads to the following definitions:
Gaussian elimination (using partial pivoting) for row reduction:
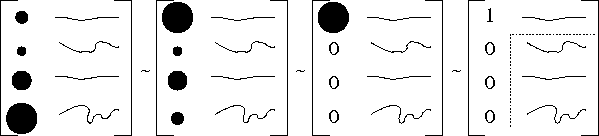
Figure 1: Here's my image of the partial pivoting process: notice that
it's recursive, and we keep paring down the size of the matrix (dotted
part in the last panel) until we run out of matrix to work on!
Example: Consider Exercise #12, p. 25. In this example, we have an augmented system of three equations in four unknowns. Hence, we know that we will not have enough information to have a unique solution: the question then is whether we are consistent, and how to express the solution set.
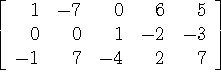
Our author suggests solving systems by pushing all the way to reduced echelon form. Here's his process for using row reduction to solve a linear system:
Example: #7, p. 25 (what's the geometry like?)
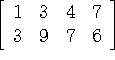
General solutions of linear systems are hence given parametrically. If there is a free variable, then there are an infinite number of solutions. If there is a row having its pivot position in the rightmost column, then the system is inconsistent. This is the essence of Theorem 2, p. 24.
Additional problems: #15, #29, #30