Section 1.5: Solution Sets of Linear Systems

Abstract:

This section shows us how to think of the solution set of a linear system geometrically, in terms of vectors. The main trick is to find the solution of a related system, the homogeneous system, and then find a particular solution to the system.

The solutions are some sorts of parametric representations of points (if only a trivial solution of the homogeneous equation exists), lines, planes, hyper-planes, etc.

The homogeneous equation tex2html_wrap_inline500 has a nontrivial solution (that is, other than the zero vector tex2html_wrap_inline502 ) if and only if the system of equations has at least one free variable.

Theorem 6: Suppose the equation tex2html_wrap_inline504 is consistent for some given vector tex2html_wrap_inline506 , and let tex2html_wrap_inline508 be a particular solution. Then the solution set of tex2html_wrap_inline504 is the set of all vectors of the form tex2html_wrap_inline512 , where tex2html_wrap_inline514 is any solution of the homogeneous equation tex2html_wrap_inline500 .

Example: Proof (by linearity): #25, p. 56

  1. (Show that tex2html_wrap_inline518 a solution.)

    Suppose tex2html_wrap_inline508 is a solution of tex2html_wrap_inline504 , so that tex2html_wrap_inline524 . Let tex2html_wrap_inline514 be any solution of the homogeneous equation tex2html_wrap_inline500 , and let tex2html_wrap_inline512 . Show that tex2html_wrap_inline518 is a solution of tex2html_wrap_inline504 .

  2. (Show that tex2html_wrap_inline518 the only type of solution.)

    Let tex2html_wrap_inline518 be any solution of tex2html_wrap_inline504 , and define tex2html_wrap_inline542 Show that tex2html_wrap_inline514 is a solution of tex2html_wrap_inline500 . This shows that every solution of tex2html_wrap_inline504 has the form tex2html_wrap_inline512 , with tex2html_wrap_inline508 a particular solution of tex2html_wrap_inline504 and tex2html_wrap_inline514 a solution of tex2html_wrap_inline500 .

Example: #8, p. 55 [

array176

]

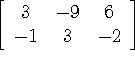
Example: #9, p. 55 tex2html_wrap_inline560

Summary

You might relate the solutions of these equations to your history from calculus as follows:

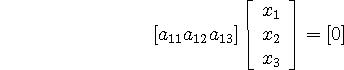
displaymath480

is the same as

displaymath481

It says that the row vector (which we might call tex2html_wrap_inline562 ) is perpendicular, or orthogonal, to the solution vector tex2html_wrap_inline564 .

Then

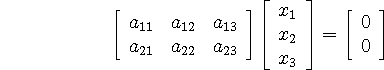
displaymath482

is the same as

displaymath481

and

displaymath484

i.e., that the tex2html_wrap_inline564 is orthogonal to both row vector ( tex2html_wrap_inline562 and tex2html_wrap_inline570 ).

Now if

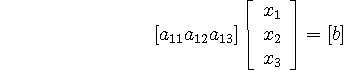
displaymath485

this says that

displaymath486

That is, that the projection of tex2html_wrap_inline564 onto tex2html_wrap_inline562 is equal to b

You remember what this means: that

displaymath487

where tex2html_wrap_inline576 is the angle between the vectors. Hence

displaymath488

says: ``the projections of x onto the rows of A make up the components of tex2html_wrap_inline506 '', and if

displaymath489

then tex2html_wrap_inline564 is orthogonal to every row of A; or, alternatively

``x is orthogonal to the span of the row vectors of A''.

The bang is still this: the solution set of tex2html_wrap_inline504 is the set of all vectors of the form tex2html_wrap_inline512 , where tex2html_wrap_inline514 is any solution of the homogeneous equation tex2html_wrap_inline500 .

Example: #35, p. 56

Example: #37, p. 56 - assumptions matter!


Wed Jan 30 11:08:21 EST 2008