MAT225 Section Summary: 2.2

The Inverse of a Matrix

Summary

The inverse of a matrix is analogous to the multiplicative reciprical: we want to solve tex2html_wrap_inline255 , and so we'd like to say that tex2html_wrap_inline257 - but we don't know how to say that with matrices! Let's find out....

First of all, this concept only applies when matrices are square: so only tex2html_wrap_inline259 matrices could possibly be invertible.

Definition: inverse An tex2html_wrap_inline259 matrix A is invertible if theres exists an tex2html_wrap_inline259 matrix C (the inverse of A) such that

displaymath245

The inverse C is denoted tex2html_wrap_inline273 , and is unique. A square matrix for which the inverse fails to exist is called singular.

A simple formula exists for the inverse of a two-by-two matrix: if A is given by

displaymath246

then, provided tex2html_wrap_inline277 ,

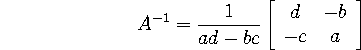
displaymath247

Otherwise, A is singular. The quantity ad-bc is called the determinant of A: det(A)=ad-bc.

#1, p. 126 (check!)

Theorem 5: if A is invertible, then tex2html_wrap_inline255 has a unique solution for each tex2html_wrap_inline291 : tex2html_wrap_inline293 .

#5, p. 126 (check!)

Theorem 6:

  1. If A is invertible, then tex2html_wrap_inline297 .

    (Check #1).

  2. If A and B are tex2html_wrap_inline259 invertible matrices, then so is AB, and the inverse of AB is the product of the inverses, in the reverse order:

    displaymath248

    More generally, the inverse of a product of any number of invertible matrices is the product of the inverses in reverse order.

    #15, p. 126.

  3. If A is invertible, then so is tex2html_wrap_inline311 , and the inverse of tex2html_wrap_inline311 is the transpose of tex2html_wrap_inline273 :

    displaymath249

Definition: an elementary matrix is one that is obtained by performing a single elementary row operation on an identity matrix. Each elementary matrix is invertible.

If an elementary row operation is performed on an tex2html_wrap_inline317 matrix A, the resulting matrix can be written as EA, where the tex2html_wrap_inline323 matrix E is created by performing the same row operation on tex2html_wrap_inline327 .

#28, p. 127

Theorem 7: tex2html_wrap_inline259 matrix A is invertible if and only if A is row equivalent to tex2html_wrap_inline335 . The elementary row operations that transform A into tex2html_wrap_inline335 simultaneously transforms tex2html_wrap_inline335 into tex2html_wrap_inline273 .

Theorem 7 suggests a method for finding tex2html_wrap_inline273 : row reduce the augmented matrix tex2html_wrap_inline347 . If A is row equivalent to tex2html_wrap_inline335 , then tex2html_wrap_inline347 is row equivalent to tex2html_wrap_inline355 .

#1, p. 126

#18, p. 126

#19, p. 126

#21, p. 126

Note : tex2html_wrap_inline273 is generally not calculated: we don't need to know its entries to solve tex2html_wrap_inline255 (similar to the notion that we don't need to row reduce to reduced row echelon form to solve: we can stop with a triangular matrix).

LONG ANDREW E
Sat Jan 29 20:54:45 EST 2011