MAT225 Section Summary: 2.4

Partitioned Matrices

Summary

The basic idea is to create and study matrices whose elements are matrices - that might seem to be compounding pain with pain, but is actually quite useful.

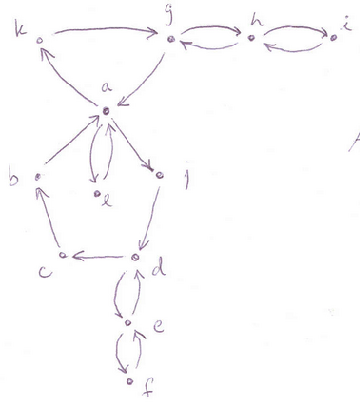
For example, in the ``proof graph'' of Theorem 8 of section 2.3,

 

we might isolate the nodes making up the pentagonal cycle (a, b, c, d, and j) and form a partitioned matrix

 

The matrix in the upper left-hand corner is a ``permutation matrix'', because it simply permutes the elements of the set of nodes a, b, c, d, and j. By contrast to the whole matrix, this matrix can be multiplied by itself as long as you want, and you will never get a ``full'' matrix (a matrix with few zeros): you will always get a matrix with exactly five non-zero elements.

Matlab code of this permutation matrix

Note that the remaining matrices also have well-defined meanings pertaining to different ``activities'' among the nodes:

• matrix E stands for ``etcetera'': connections among the nodes other than a, b, c, d, and j;
• matrix G represents connections from the nodes a, b, c, d, and j to the others; and
• matrix H represents connections from the others to the nodes a, b, c, d, and j.

If either of G or H are zero matrices, then the nodes (representing different statements) will not have been shown to be equivalent, because, though we may be able to get from one group of nodes to the other, we won't be able to get back.

Examples: #2 and 3, p. 139

The other really neat thing that this section presents is the idea of matrix multiplication as a sum of outer-products. Recall the definition of an outer-product of two vectors and . We can form two outer-products from these two vectors: and .

So a matrix product AB can be thought of as

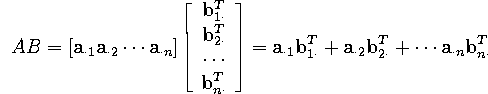
(where the `` '' in the indices indicates which of rows or columns is being chosen - if the dot occurs first, it's a column; second, it's a row).

Example: #17, p. 140