MAT225 Chapter 3 Summary

Determinants

As a preface, note that we're always talking about square matrices in the following.

1. Theorems/Formulas

   Theorem 2, p. 189: If A is a triangular matrix, then det A is the product of the entries on the main diagonal of A.

   Theorem 3, p. 192: Let A be a square matrix.

   1. If a multiple of one row of A is added to a different row to produce a matrix B, then det B= det A.
   2. If two rows of A are interchanged to produce B, then det B= -det A.
   3. If one row of A multiplied by k to produce B, then det B=k det A.
   These are the operations of elementary matrices, so we see how to relate the determinant of the matrix U obtained by row-reduction from A to the determinant of A itself:

   Example: Let's check Theorem 3 against 2 by 2 matrices.

   Formula (1), p. 194: Suppose a square matrix A has been reduced to an echelon form U by row replacements and r row interchanges. Then

   

   Since U is triangular, its determinant is simply the product of its diagonal entries.

   Theorem 4, p. 194: A square matrix A is invertible if and only if .

   Theorem 5, p. 196: If A is an matrix, then det det A.

   Theorem 6, p. 196: If A and B are matrices, then det AB= (det A)(det B).

2. Properties/Tricks/Hints/Etc.

   In the ball of unit volume (that is, a ball centered at the origin of volume 1) is transformed under a linear transformation into an ellipsoid. The volume of the ellipsoid is the absolute value of the determinant. If you like, you can consider that the definition of the determinant! See the figure on page 209.

3. Summary

   We first encountered the determinant when inverting matrices: it appears in the formula

   

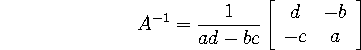
   The determinant is denoted det A, and det A=ad-bc. Obviously if det A=0, then the matrix is not invertible, so the determinant was mixed up with the idea of invertibility.

   The determinant was important classically, perhaps more so than it is today. The idea of cofactors is classical, elegant, but not particularly practical. As mentioned in the text, the calculation of a determinant is carried out by the method of LU decomposition, and relies upon the simple fact that the determinant of a triangular (and especially diagonal) matrix is the product of the diagonal elements.

   This is certainly the most important fact: the determinant represents the volume of the image of the ball of unit volume under the linear transformation represented by . So if the determinant is zero, the ball's image has been ``squashed'' so that it has zero volume. This means that the matrix is singular, and cannot be inverted. This is the key fact, and the fact that we will encounter again when we bump up against eigenvalues.