MAT225 Section Summary: 4.3

Linearly independent sets; bases

Summary

We're accustomed to writing vectors in terms of a set of fixed vectors: for example, in two-space we write every vector in terms of vectors tex2html_wrap_inline290 and tex2html_wrap_inline292 . Each vector has a unique representation in terms of these two vectors, which is important. This set of two vectors is called a basis of two-space: it is enough vectors to write each vector of the space in terms of it, but not so many vectors that there are multiple representations of each vector. These are the two important properties: spanning the space, and avoiding any redundency. That is, a basis is the smallest spanning set possible. It is also the largest set of linearly independent vectors: any more, and you'd have dependence.

linear independence: An indexed set of vectors tex2html_wrap_inline294 in V is said to be linearly independent if the vector equation

displaymath284

has only the trivial solution ( tex2html_wrap_inline298 ). The set is linearly dependent if it has a nontrivial solution.

Example: #4, p. 243 (independence)

Theorem 4: An indexed set tex2html_wrap_inline294 of two or more vectors, tex2html_wrap_inline302 , is linearly dependent tex2html_wrap_inline304 some tex2html_wrap_inline306 (j>1) is a linear combination of the preceding vectors tex2html_wrap_inline310 .

Example: #33, p. 245

Basis: Let H be a subspace of a vector space V. An indexed set of vectors tex2html_wrap_inline316 in V is a basis for H if

  1. B is a linearly independent set, and
  2. the subspace spanned by B coincides with H; that is,

    displaymath285

Example: #4, p. 243 (basis)

Example: #34, p. 245

Example: The columns of the tex2html_wrap_inline328 identity matrix tex2html_wrap_inline330 for a basis, called the standard basis for tex2html_wrap_inline332 :

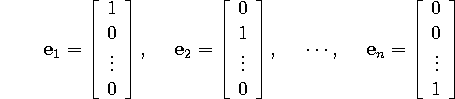
displaymath286

In three-space these are simply the vectors tex2html_wrap_inline290 , tex2html_wrap_inline292 , and tex2html_wrap_inline338 .

Theorem 5 (the spanning set theorem): Let tex2html_wrap_inline340 be a set in V, and let tex2html_wrap_inline344 .

  1. If one of the vectors in S - say tex2html_wrap_inline348 - is a linear combination of the remaining vectors in S, then the set formed from S by removing tex2html_wrap_inline348 still spans H.
  2. If tex2html_wrap_inline358 , some subset of S is a basis for H.

Theorem 6: the pivot columns of a matrix A form a basis for Col A.

Turns out that elementary row operations on a matrix do not affect the linear dependence relations among the columns of the matrix. Hence, the reduced matrix has the same independent columns as the original matrix. Make sure to choose the columns of the matrix A, however, rather than the reduced matrix....

Example: #36, p. 245

LONG ANDREW E
Sat Jan 29 20:56:44 EST 2011