Orthogonal Projections
Summary
This section formalizes one of the things that I've been emphasizing all along
about projections, orthogonal complements, etc., to whit: we can't solve the
equation ![]() , so we try to solve the next best thing: we solve
, so we try to solve the next best thing: we solve
![]() , where
, where ![]() is the projection of
b onto the column space of A.
is the projection of
b onto the column space of A.
Theorem 8: The Orthogonal Decomposition Theorem Let W be a subspace of
![]() . Then each y in
. Then each y in ![]() can be written uniquely in the form
can be written uniquely in the form
![]()
where
![]() is in W and
is in W and ![]() is in
is in ![]() . In fact, if
. In fact, if
![]() is any orthogonal basis of W, then
is any orthogonal basis of W, then
![]()
and then ![]() .
.
orthogonal projection of y onto W: The vector ![]() is
called the orthogonal projection of y onto W, written
is
called the orthogonal projection of y onto W, written ![]() .
.
Properties of orthogonal projections:
Theorem 9: The Best Approximation Theorem Let W be a subspace of
![]() , y any vector in
, y any vector in ![]() , and
, and ![]() the orthogonal
projection of y onto W. Then
the orthogonal
projection of y onto W. Then ![]() is the closest point
in W to y, in the sense that
is the closest point
in W to y, in the sense that
![]()
for all v in W distinct from ![]() .
.
Theorem 10: If ![]() is an orthonormal
basis for a subspace W of
is an orthonormal
basis for a subspace W of ![]() , then
, then
![]()
If ![]() , then
, then
![]()
for all y in ![]() .
.
Now, as an example, I want to consider Taylor series expansions for function with three derivatives at a point a (that might define our space: you should check that this is indeed a vector space, by checking that it's a subspace of the space of thrice differentiable functions). The Taylor series expansion for the function f is
![]()
This is a vector in the space ![]() . What we're doing is
projecting the vector f (which is otherwise unspecified) onto
. What we're doing is
projecting the vector f (which is otherwise unspecified) onto ![]() ,
in a way that minimizes the distance between the vectors
,
in a way that minimizes the distance between the vectors
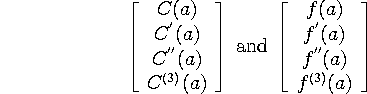
(in fact, the difference between these vectors is zero!).
Now with functions you have to be a little careful, because it's a little
tricky to define just what is meant by an inner-product. We're not going to get
into that...!