MAT225 Section Summary: 7.1

Diagonalization of Symmetric Matrices

Summary

As we begin chapter seven, we should keep track of our specific objectives: we're interested in two goals:

1. we're examining the actions of symmetric matrices as linear transformations, and
2. we're interested in analyzing the structure of general matrices of information (like images, say, as described in the opening pages of the chapter, p. 447).

Great things happen when you find yourself working with symmetric matrices. Their special structure leads to some seemingly magical properties, as we see here. Symmetric matrices are obviously an important special case, as we found in working with the least-squares problems (where the left-hand side was , a symmetric matrix!).

Theorem 1: If A is symmetric, then any two eigenvectors from different eigenspaces are orthogonal.

Example: #13, p. 454

orthogonally diagonalizable: A matrix is orthogonally diagonalizable if there is an orthogonal matrix P and diagonal matrix D such that

Example: #22, p. 454

Theorem 2: is orthogonally diagonalizable if and only if A is a symmetric matrix.

The Spectral Theorem: Symmetric has the following properties:

1. A has n real eigenvalues, counting multiplicities (no complex eigenvalues!).
2. The dimension of the eigenspace for each eigenvalue equals the multiplicity of as a root of the characteristic equation (no ``missing'' dimensions).
3. The eigenspaces are mutually orthogonal: eigenvectors corresponding to different eigenvalues are orthogonal.
4. A is orthogonally diagonalizable.

Example: #31, p. 455

Since , where p is an orthogonal matrix, we can write

the spectral decomposition of A. Each matrix is a projection matrix: the projection of vector x onto the subspace spanned by is given by

(the last part of the equation is one way of thinking of the projection that I've emphasized).

Example: #34, p. 455

The action of A as a linear transformation is well understood, therefore:

or

That is, we project x onto each basis vector, and then multiply each of these projections by the corresponding eigenvalue. Alternatively, if

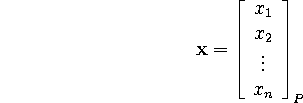
where P represents the basis composed of its columns, then

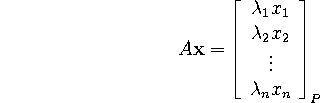
Neat!