The Singular Value Decomposition (SVD):
Fundamental Theorem of Linear Algebra
Summary
That's right: The Fundamental Theorem of Linear Algebra. The SVD ties it all together. Rather than focus on the technicalities, I want to focus on the ``bang''. If you can understand the Singular Value Decomposition, then you understand this course. If you are weak in any part, then you will not really understand this theorem. Understanding this section is the best preparation for the final exam.
The Singular Value Decomposition: Let A be an ![]() matrix with
rank r. There exists
matrix with
rank r. There exists
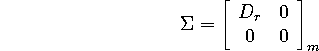
for which D is diagonal, with positive entries (the singular values)
![]() , and
, and
![]()
The 0 matrices are included simply to pad D (if necessary) to make the
dimensions right. Here is ![]() with the dimensions indicated explicitly:
with the dimensions indicated explicitly:
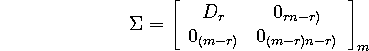
For example, if A happens to be invertible, then there are no zero matrices,
and ![]() .
.
Now your first impulse might be to say ``so what?'' (But don't say it in my hearing!) Understanding this is the true key to understanding A either
You might also want to know what this has to do with all the symmetric matrices we've been looking at: the connection is crucial. One way that the SVD arises is by considering the problem of solving a constrained optimization problem:
What is the maximum value of ![]() given that
given that ![]() ?
?
Solving this is equivalent to solving the problem
What is the maximum value of ![]() given that
given that ![]() ?
?
But this is equivalent to solving
What is the maximum value of ![]() given that
given that
![]() ?
?
So it's equivalent to solving a problem about constrained optimization of quadratic forms....
Now, to make my life easy, I'm going to think of ![]() (A is rectangular,
and its ``height'' is greater than or equal to its ``width'').
(A is rectangular,
and its ``height'' is greater than or equal to its ``width'').
The matrix ![]() is positive semi-definite: that is, it has positive
(
is positive semi-definite: that is, it has positive
( ![]() ) eigenvalues, which we can calculate as
) eigenvalues, which we can calculate as
![]()
Now, here's a curious fact, which I'm going to gloss over entirely (in order to
get to the ``bang!''): ![]() (which is also positive semi-definite) can be
orthogonally diagonalized as
(which is also positive semi-definite) can be
orthogonally diagonalized as
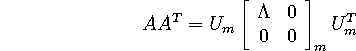
(Same ![]() ! - same eigenvalues). Again, the zero matrices are only
included to (possibly) make the dimensions work out. If r=m, then they
disappear. Now for the kicker:
! - same eigenvalues). Again, the zero matrices are only
included to (possibly) make the dimensions work out. If r=m, then they
disappear. Now for the kicker:
It's easy to check that the SVD formula recreates ![]() and
and ![]() . Give it a try!
. Give it a try!
Now the best way to think about A from the standpoint of the image problem is to throw out the irrelevant stuff, and write
![]()
where we've thrown out the eigenvectors of ![]() and the eigenvectors of
and the eigenvectors of
![]() corresponding to the zero weights of
corresponding to the zero weights of ![]() . This might be called the
reduced SVD of A. Hence we can write a decomposition analogous to the
spectral decomposition of a symmetric matrix for A, as
. This might be called the
reduced SVD of A. Hence we can write a decomposition analogous to the
spectral decomposition of a symmetric matrix for A, as
![]()
This is the matrix A composed of a sum of rank-one outer product matrices,
weighted from most important to least (by the size of ![]() ).
An example of this can be found at
http://www.nku.edu/
).
An example of this can be found at
http://www.nku.edu/ ![]() longa/classes/mat225/days/dad/Abe.jpg
longa/classes/mat225/days/dad/Abe.jpg
You know that the rank of A and ![]() is the same. The row space of
one and the column space of the other are equivalent. The SVD makes that
clear.
is the same. The row space of
one and the column space of the other are equivalent. The SVD makes that
clear.
From the standpoint of the transformation ![]() , taking a
ball in
, taking a
ball in ![]() to an ellipsoid in
to an ellipsoid in ![]() , the better way to think of A is as
, the better way to think of A is as
![]()
where by ![]() we understand the succession of transformations
we understand the succession of transformations
![]() as follows:
as follows:
![]()
(the expression of ![]() in the basis of V, as projections
onto the basis vectors). This is effectively a rotation/reflection of the unit
(radius) ball in
in the basis of V, as projections
onto the basis vectors). This is effectively a rotation/reflection of the unit
(radius) ball in ![]() into position for easy scaling.
into position for easy scaling.
![]()
represents the scaling of the vector along each of the principal axes (the
conversion of a ball into an ellipsoid), including possible squashing of some
of the dimensions corresponding to the null-space of A. The resulting
vectors are in ![]() .
.
![]()
represents the rotation/reflection of the resulting ellipsoid in ![]() so that
the result is oriented as it should be, since
so that
the result is oriented as it should be, since ![]() is not necessarily
alligned well with the standard basis. This is the image of the vector
is not necessarily
alligned well with the standard basis. This is the image of the vector
![]() in the column space of A, as a linear combination of the column
space basis U of A.
in the column space of A, as a linear combination of the column
space basis U of A.
Here's a nice picture due to Cliff Long and Tom Hern that captures these three steps, at
http://www.nku.edu/ ![]() longa/classes/mat225/days/dad/SVD.jpg
longa/classes/mat225/days/dad/SVD.jpg
The rank of a matrix is equal to the number of non-zero singular values. The
condition number (or at least the most common definition of it) is given
as the ratio of the largest to smallest singular values (infinity if rank ![]() , since it's as if the matrix has a singular value of 0).
, since it's as if the matrix has a singular value of 0).
It is all really too marvellous for words. We'll need to look at some pictures, and a few example problems.
Example: #15, p. 481
Note: in order to calculate the SVD of a matrix, you need only find D and
either U or V - you don't need both. That's because if ![]() ,
then if we know D and V, then
,
then if we know D and V, then ![]()
This leads to the idea of a pseudo-inverse of a matrix:
![]()
This is the closest thing to an inverse that a general matrix A has!
There's a nice picture due to Cliff Long and Tom Hern at
http://www.nku.edu/ ![]() longa/classes/mat225/days/dad/pseudo.jpg
longa/classes/mat225/days/dad/pseudo.jpg
Example: #9, p. 481