- Math Club -- tonight!
- Read Section 8.6 for next time, responding to the worksheet for section 8.6;
- Prepare for a quiz next time on the content of section 8.6.
- Calc lab (ST 243) hours:
Mondays: 8:30am- 1:45pm Tuesdays: 10:45am- 1:30pm Wednesdays: 8:30am-12:30pm Thursdays: 10:45am- 4:00pm Fridays: 8:30am-12:00pm
- What's integration all about? Well, we usually start by going about calculating (signed) areas:
"dA" is called an "infinitesimal" -- it's a tiny chunk of area -- tinier than anything you know ("vanishingly small")!
What's numerical integration all about? We do pretty much the same thing, only we have
where the
are small, but not vanishingly small.
- There are various schemes for numerical integration:
- Left Rectangular
- Right Rectangular
- Midpoint
- Trapezoidal
- Simpson's rule.
- Three of the rules are so called "rectangle rules" (LRR, RRR, Midpoint Rule);
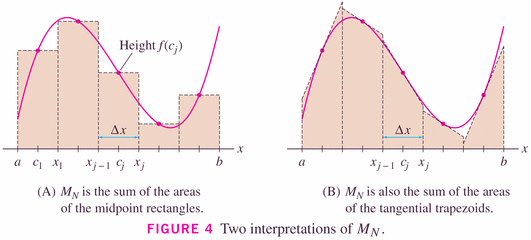
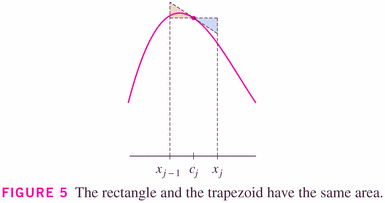
but as the image to the right (above) and the graphical insight on p. 415 show, we can think of the Midpoint rule as being a "Tangent rule":

- The Trapezoidal rule is really just the average of the LRR and RRRs. This gives rise to an important observation, which I want to encourage you to think about, and here it is:
When you have two estimates, you have a third. (their arithmetic average, in this case).

- Simpson's rule is a "blend" (or weighted average) of the Midpoint
and Trapezoidal rules, which perfectly balances the errors of the two
to generate a better rule:
Notice that the number of subintervals in Simpson's rule must be even.
Now we can go further:
When you have two estimates, you have infinitely more. (their weighted arithmetic averages).
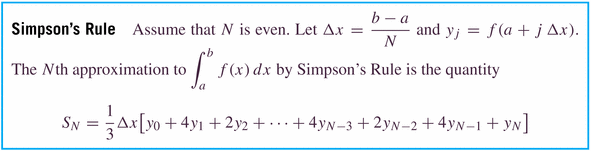


- Last time we tried a hand out which emphasizes this message. I'd like to revisit this
- Check midpoint calculation
- Let's do the calculations by the formulas, for
- Trapezoid
- Simpson's
- Check that we get the same things using the averages
- Calculate the true value of the integral, and compare to the approximations. What's surprising?
- Setting up your calculator for numerical integration
- Examples:
- #9, p. 421
- #41, p. 422
- Links:
- Here's a nice summary of the issue, focused on the use of Mathematica to illustrate them. Interesting even if you don't use Mathematica.