Today:
- Announcements:
- We have an exam next time, which will be through 8.1.
- I've posted all the old quizzes from this term.
Material to be covered for Exam 2:
- Chapter 5:
- 5.2: pp. 188, 189, #1, 5
- Sampling distribution of the sample proportion (p), mean and standard error (p. 181)
- special rule for checking normality (proportions must fall between 0 and 1, p. 184)
- Z-statistic for a proportion (p. 186)
- 5.3: pp. 201, 202, #1, 3
- Making inferences about a conjectured value of
 or
or 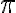 (p. 196)
(p. 196)
- 5 Review:
- Ch. 5 Review: pp. 205 - 207, #1, 2, 8
- Summary: p. 205
- Chapter 6:
- 6.1 pp. 221, 222, #2, 3, 4
- Estimating
 via a Confidence interval (known
via a Confidence interval (known  ) (p. 214)
) (p. 214)
- Good choices for Z (90%, 95%, 99%) (p. 212)
- Validity of the z-interval (p. 215)
- Procedure to follow, p. 221
- 6.2 227 1, 3
- Selecting the sample size (p. 224)
- 6 Review:
- Ch. 6 Review 229 - 231 1, 3, 8
- Summary, p. 229
- Chapter 7:
- 7.1: pp. 242, 243, #3, 5
- Elements of a test of a hypothesis (p. 234)
- Null and alternative hypotheses
- Observed significance level (p-value)
- Test Statistic
- Decision rule
- Calculation
- Interpretation
- 7.2: pp. 255, 256, #1, 3, 4
- Performing a test of hypothesis about
 (p. 245, 246)
(p. 245, 246)
- 7.3: pp. 264, #1, 2
- Possible errors (type I and type II)
- 7 Review:
- Ch. 7 Review: pp. 269, 270, #2, 3, 4
- Summary, p. 267
- Chapter 8:
- 8.1: pp. 284 - 286, #3, 5, 7
- Inferences about a population proportion
Section 8.1: Inferences about a population proportion 
- Confidence intervals: Essentially the same as for the sample mean, but
- Hypothesis testing: Essentially the same as for the sample mean,
except that you have a different formula for the z-statistic:
}{n}}}})
- Additional sample proportion example: #4, p. 285
Section 8.2: Estimating
 when
when
 is unknown
is unknown
- We finally get real! We don't know
 in general. So we're going to be estimating it....
in general. So we're going to be estimating it....
- The t-distribution
- similar in shape to the normal
- we estimate
 using the sample standard deviation, s:
using the sample standard deviation, s:
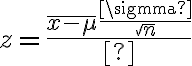 |
whereas |
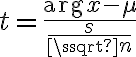 |
- Properties of the t-distribution above:
- symmetric, like the normal
- centered at zero, like the normal
- had n-1 degrees of freedom
- the standard deviation of the distribution is

- Since the standard deviation of the distribution is
greater than 1, it is a little broader than the normal,
a little more variable.
- The major difference between the z- and t-distributions is that
for the normal we have one single table; for the t-distribution, we need to
know the value of n, and then use the table for that value of
df=n-1. (Rats!) Of course, with technology, this is not really much of a
problem....
- How does this affect our strategy? It's basically the same: see
page 290....
- Let's try an example:
Links
Website maintained by Andy Long.
Comments appreciated.
in this problem, so we can't actually do a test of hypothesis (yet!;). On the other hand, we can hope that s is a good approximation to
, so we can imagine that
. Since 5 is about 9 standard errors from 5.9, we're pretty likely to conclude (using any confidence!) that the bags are heavier than 5 pounds on average.