Day 19 in MAT227

Last time: Section 7.7: L'Hopital's Rule

Next time: Section 8.2: Integration by Parts

Today:

Announcements:
- Homework assignment 7.3 returned
  - #19 -- don't forget ${\pm}$ (many of you made an illegal step, because you forgot the caution in properties of logs....
  - #47 -- Almost everyone got this right! Tangent line is one of the most important animals in calculus -- are you relying on the back of the book, or the back of your hand?
  - #85 -- two options for u ....
  - Question 3 (don't forget the questions!) -- use the mirror.
- Assignment 7.4 due today
Today: We finish section 7.7: L'Hopital's Rule (Sometimes limits are kind of tricky!)
- In financial mathematics (e.g. compound interest problems, subject of section 7.5, which we're not covering!), we tend to use an unusual base for an exponential:
  
  ${P(t)=P_0\left(1+\frac{r}{n}\right)^{nt}}$
- You may have encountered a few laws such as The rule of 72 (70, 71, 69.3,...) to calculate doubling time: forget them! Just do the math: the question is
  
  For what value of t is ${P(t)=P_0\left(1+\frac{r}{n}\right)^{nt}=2P_0}$ ?
  
  Solving t is ${P_0\left(1+\frac{r}{n}\right)^{nt}=2P_0}$ for t, we get
  ${t=\frac{\ln 2}{n\ln(1+\frac{r}{n})}}$
  
  where n is the number of compoundings per year, and r is given as a decimal (e.g. 9% is represented by .09). This is the doubling time.
  When compounding is continuous (i.e. ${n \to \infty}$ ), this reduces to the very lovely rule
  ${\frac{\ln 2}{r}}$ which is found in your book on p. 369.
- Now, how do we know that ${\lim_{n \to \infty}\frac{\ln 2}{n\ln(1+\frac{r}{n})}=\frac{\ln 2}{r}}$ ? That is, how do we know that
  
  ${\lim_{n \to \infty} \ {n\ln(1+\frac{r}{n})}={r}}$ ?
  The answer, of course, is L'Hopital's Rule, which is useful in solving certain indeterminate limits:
  
  Let's rewrite it a little: we want to show that
  
  ${\lim_{n \to \infty}\frac{\ln(1+\frac{r}{n})}{\frac{1}{n}}={r}}$
- Here's the general situation:
- And if the limit of the quotient of the derivatives is indeterminate, then iterate -- that is, do it again! Then work with the ratio of the second (or higher) derivatives.
- Examples:
  - Demonstration that ${\lim_{h \to 0} \frac{e^h-1}{h} = 1}$ (remember that this limit figured into the definition of $f'(x),$ where $f(x)=e^x$ )
  - #2, p. 390
  - #6, p. 390
  - #20, p. 390
  - #42, p. 390
  - A better proof of the fact that
    
    (take logs! Better than induction....)
  - Proof of L'Hopital's Rule (requires the limit definition of the derivative)
Section 7.8: Inverse Trig Functions
- For example, the sine function has inverse function arcsin (note the bad notation below -- don't be confused! But our notation in mathematics is sometimes "context sensitive"):
  
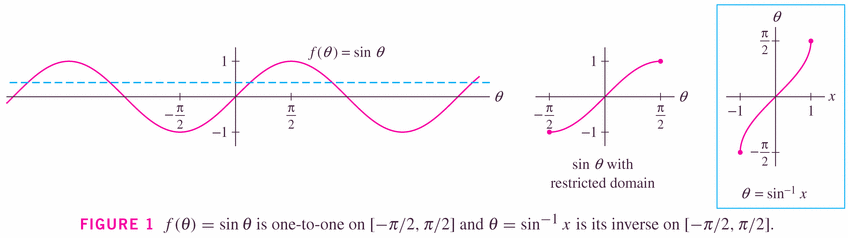
  and cosine function has inverse function arccos:
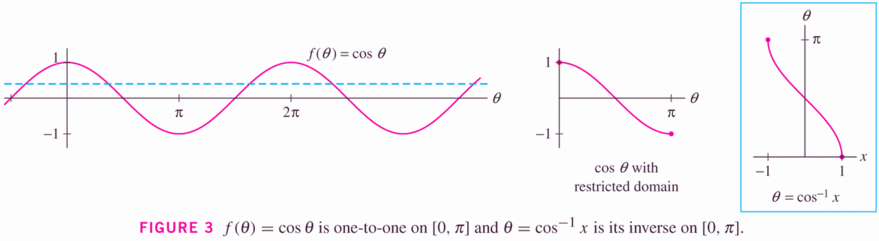
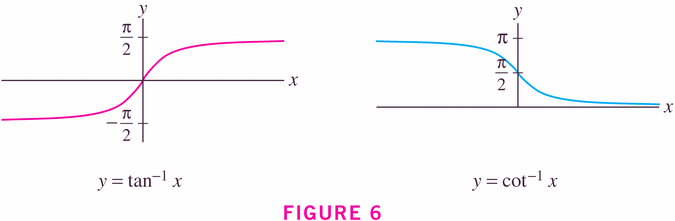
- Arctan and arccot are also sometimes useful:
- Derivatives: They're computed in the usual "sneaky" inverse function way:
  
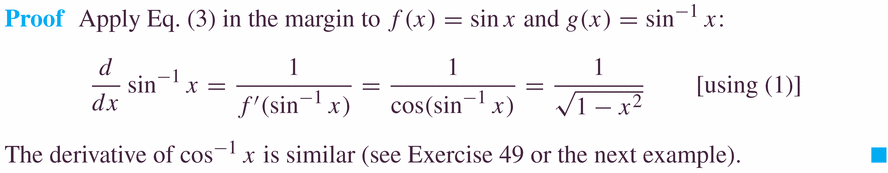
  Exercise 49, p. 398
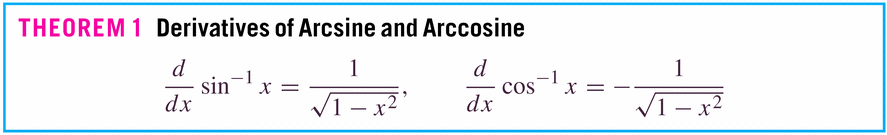
- Examples:
  - #50, p. 398
  - #85, p. 399
  - Optimal Positioning of Fixed Solar Panels

Website maintained by Andy Long. Comments appreciated.