Calculus Exercise, Day 03

1. Date
2. Question
3. Group member names
4. Solution strategy or strategies proposed.
5. Analysis of the process.

Consider this data, concerning diagnoses of HIV and other sexually transmitted diseases among homosexual men (from Macdonald, (2004). Recent trends in diagnoses of HIV and other sexually transmitted infections in England and Wales among Men who have Sex with Men -- MSM -- here's a local copy):

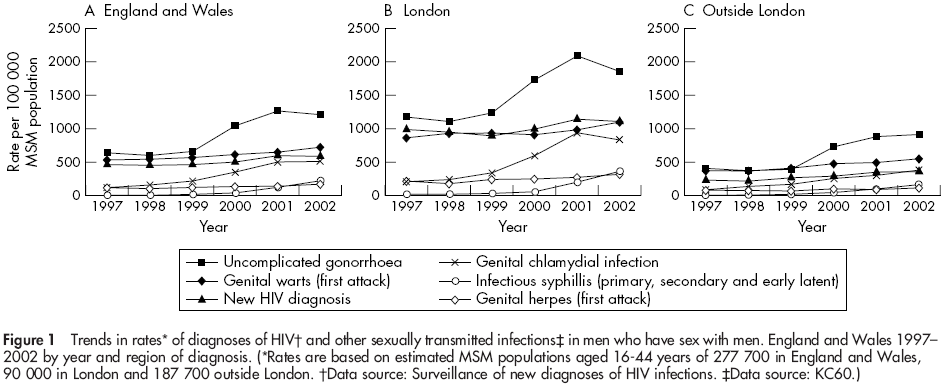
Here are my digitized data, for the years 1997-2002 (for "uncomplicated gonnorhoea" in London):

1997	1200
1998	1100
1999	1250
2000	1750
2001	2100
2002	1800

1. How do you think the authors created the curves (graphs of continuous functions) connecting the data points?

2. Once again: what do the areas under the curve mean (for "uncomplicated gonnorhoea" in London, say)? What is the scientific importance of the area? What are the physical units of the area under the curve?

3. Create several different Riemann sums for the area under the curve of the rate of "uncomplicated gonnorhoea" in London, for the years 1997-2002. Which do you like the best?

   If you look at the definition of the Riemann sum (a function of three variables! See p. 262), you see that there are three things you can alter to create a different Riemann sum: the function f, the partition P, and the choice of representative points on each subinterval (C).

4. Write each of your answers in part 3 as definite integrals; indicate the function f(t) that you refer to in each case.

5. Suppose that you were interested in breaking out your analysis, so that it covered the two periods 1997-2000, and 2000-2002. What would you want to assert about the integrals , , and

6. Once again, why can we not immediately and thoughtlessly push to the definite integral, as defined on page 263?