- Exam 1 will be Wednesday, 2/10, and will cover through continuity (section 17).
- Return of homework sets
- p. 25: graded 2, 7, 9
- #7
- #9: z0 is not an open set!
- p. 35
- p. 25: graded 2, 7, 9
- Today's activity, and new assignment:
Fri 2/5 14-16 - Read sections 16, 17
- Problems pp. 53, #2ac, 4, 5, 7, 10, 12 (Due with exam 1, Wed, 2/10)
- Summary sheet of
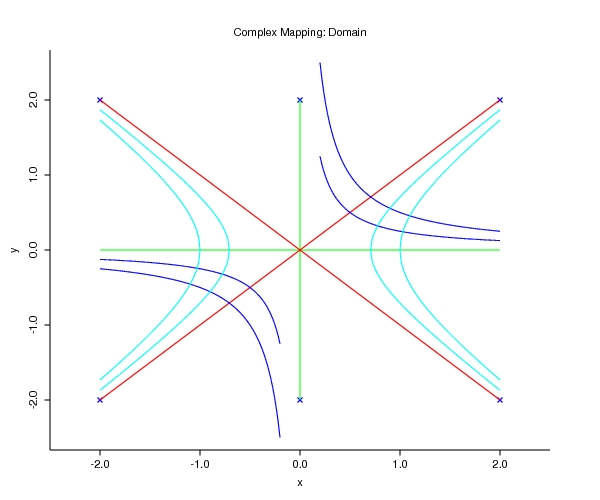
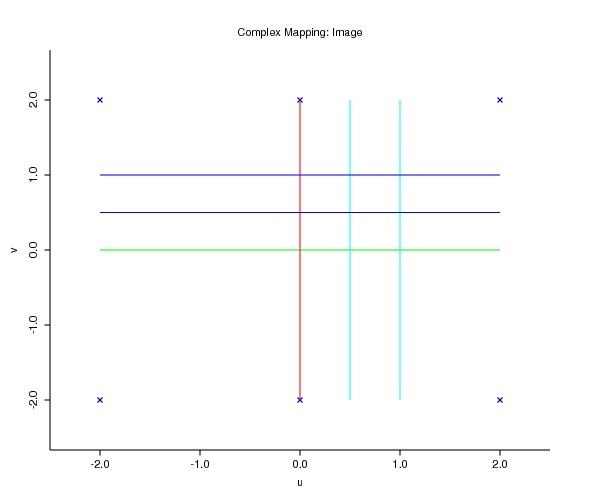
- Summary sheet of
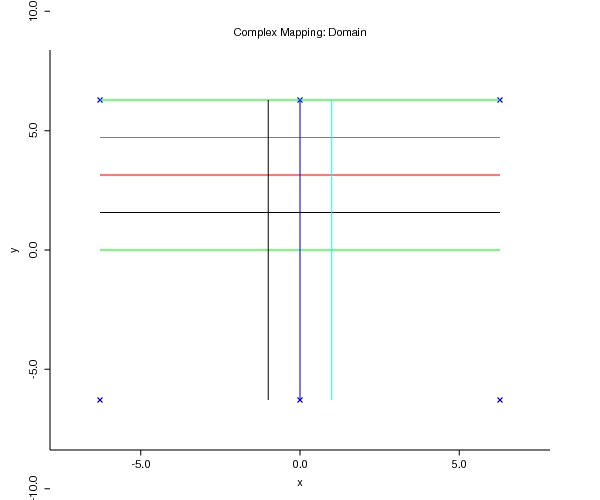
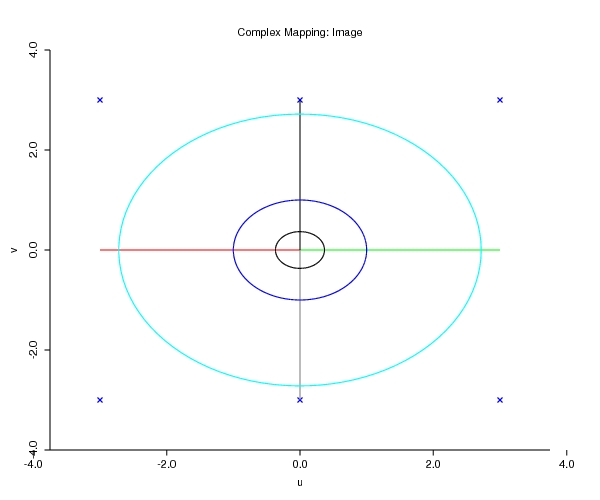
- Definition
- Note: extension to "one-sided" limits (Example 1, p. 44)
- Limits are unique
- Examples, using the definition
- Reciprocal of Example 2, p. 45
- 2b, p. 53
- (Limits exist) iff (limits of components exist)
- Given that limits of f and g exist at z0. Then limits of sums, products, and quotients exist, as expected (usual caveat for quotients -- denominator doesn't go to zero)
- We extend the complex plane by adding the point at infinity!?
- Riemann sphere (p. 49), and the stereographic projection between the complex plane and the Riemann sphere.
- An
neighborhood of infinity is the set of points
- To end class today, I'd like to see if we can make the correspondence between points and the plane and points on the sphere explicit, by coming up with an equation for the one-to-one correspondence.