Day 16, MAT115

Last Time

Next Time

Announcements:
- No assignment due this week. I'll post a new assignment on Friday, concerning bases.
- New reading assignment: make sure that you read about the Mayans, and their base 20 system.
Today's Topic: Busting up numbers (bases)
- Question of the day(s): What other civilizations used curious bases?
- How can we understand representations in different bases?
  - A base is a natural number, a counting number, larger than 1.
  - Each number is written using only powers of that base, starting from the power 0 (since anything to the power 0 is 1): for example,
    - ${2^0,2^1,2^2,2^3,\ldots}$
    - ${8^0,8^1,8^2,8^3,\ldots}$
  - There are as many digits as the base: so base two uses only two digits (0 and 1); base 10 uses only 10 digits (0 through 9).
  - The number is written so that each digit falls in a place, which represents a unique power of the base.
- The Great Fraudini writes numbers in base 2 (see p. 11 of our text) -- that is, using powers of two.
  
  197
  57
  
  How would we write these numbers in base 2?
  
  197
  
  57
- Last time we saw how the hexadecimal (base 16) system is used in web pages, to create colors using values for red, green, and blue (RGB, written as a string of "digits" in hex). The color for this page is #FFF8DC.
- Translating between bases
  - Write 253 (written here in base 10) in base 2
  - Write 100101101₂ (written here in base 2) in base 10
  - Write 253 (written here in base 10) in base 8
  - Write 100101101₈ (written here in base 8) in base 10
  - Write 253 (written here in base 10) in base 16
  - Write 100101101₁₆ (written here in base 16) in base 10
- The Mayans used a curious number system:
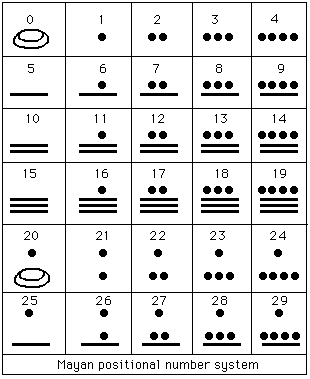
  Your reading assignment is to inform you a little more about this curious system. You will learn a little about the famous Mayan calendar.
- Now: let's play detective in the times of Babylon.....
  - "...a cuneiform tablet measuring perhaps 3 inches by 5. The markings can be made by pressing the end of a cut reed into wet clay. Dating such a tablet is seldom easy. The appearance of this tablet suggests that it may have been made in Akkad in the city of Nippur in the year -1700, about 3700 years ago."
  - Answer the author's three questions:
    1. What is this and what are its properties?
    2. What was its original purpose?
    3. What does this tell me about the culture that produced it?

Links:

Mayan calendar conversions

Website maintained by Andy Long. Comments appreciated.